6 Tópicos em Estatística Computacional
6.1 Geração de Números Pseudo-Aleatórios
O conteúdo para esse tópico entra-se em PDF e poderá ser acessado aqui. Em um futuro próximo, essa seção será reescrita e fará parte do corpo deste HTML.
6.1.1 Método da Transformação Inversa (Caso Discreto)
O método da transformação inversa também poderá ser aplicado também para gerar observações de v.a.’s discretas. Seja \(X\) uma v.a. discreta, tal que
\[... < x_{i-1} < x_i < x_{i+1} <\, ...\,.\] As observações acima são pontos de descontinuidade de \(F_X(x)\). Então, a transformação inversa é \(F_X^{-1} = x_i\), quando \(F_X(x_{i-1}) < u \leq F_X(x_i)\). O algoritmo que segue poderá ser utilizado para gerar observações de \(X\).
Algoritmo:
- Gere um número pseudo-leatório \(u\) de uma v.a. \(U \sim \mathcal{U}(0,1)\);
- Retorne \(x_i\) como observação de \(X\), tal que \(F(x_{i-1}) < u \leq F(x_i)\).
Em outras palavras, gere \(u\) de uma v.a. \(U \sim \mathcal{U}(0,1)\) e compare na sequência:
- Se \(u < p_0\), faça \(X = x_0\) e pare;
- Se \(p_0 \leq u < p_0 + p_1\), faça \(X = x_1\) e pare;
- Se \(p_0 + p_1\leq u < p_0 + p_1 + p_2\), faça \(X = x_2\) e pare;
- …
- Se \(\sum_{i = 0}^{j-1} p_i \leq u < \sum_{i=0}^j p_i\), faça \(X = x_j\) e pare;
- …
em que \(p_j = P(X = j)\).
Exemplo: Implemente, em R, uma função que retorna a quantidade de observações de uma v.a. \(X\) com função de probabilidade:
\[P(X = 1) = 0.3, P(X = 2) = 0.2, P(X = 3) = 0.35, P(X = 4) = 0.15.\]
random <- function(n = 1L){
x <- 1L:4L
probs <- c(0.3, 0.2, 0.35, 0.15)
u <- runif(n = n, min = 0, max = 1)
# Criando uma função para ser passada à um funcional.
comp <- function(u){
# Retorna a primeira ocorrência de TRUE
match(TRUE, u < cumsum(probs))
}
purrr::map_dbl(.x = u, .f = ~ comp(.x))
}
set.seed(0)
random(n = 10L)## [1] 4 1 2 3 4 1 4 4 3 3Em um estudo de simulação, poderemos ter interesse em gerar observações equiprováveis, em que a v.a. \(X\) assume um número finito de observações, tal forma que:
\[P(X = j) = \frac{1}{n}, \,\, j = 1, 2, \ldots, n.\] Porém, note que para esse caso, não precisaremos fazer muitas comparações, uma vez que sabemos que \(x = j\) quando \(u \leq \frac{j-1}{n}\). Sendo assim, tomamos \(x = j\) quando \(nu \leq j - 1\).
Note que fazer \(x = j\) quando \(nu \leq j - 1\) equivale a fazer \(x = \mathrm{Int}(nu) + 1\), em que \(\mathrm{Int}(\cdot)\) aqui irá retornar o menor inteiro de um número.
Exemplo: Seja \(X \sim Bernoulli(p)\), em que \(P(X = 0) = 1 - p\) e \(P(X = 1) = p\), com \(0\leq p \leq 1\). A função rbernoulli(n = 1L, p) retorna possíveis observações de \(X\).
rbernoulli <- function(n = 1L, p){
u <- runif(n = n, min = 0, max = 1)
comp <- function(x){
ifelse(x < 1 - p, 0L, 1L)
}
purrr::map_int(.x = u, .f = ~ comp(.x))
}
set.seed(0) # Fixando uma semente.
n <- 1e4 # Número de observações.
result <- rbernoulli(n = n, p = 0.6) # prob. de sucesso = 0.6.
# Probabilidade de sucesso aproximada.
sum(result == 1)/n## [1] 0.59736.1.2 Método da aceitação e rejeição
Em situações em que não podemos fazer uso do método da inversão (situações em que não é possível obter a função quantílica) e nem conhecemos uma transformação que envolve uma variável aleatória ao qual sebemos gerar observações, poderemos fazer uso do método a aceitação e rejeição.
Suponha que \(X\) e \(Y\) são variáveis aleatórias com função densidade de probabilidade (fdp) ou função de probabilidade (fp) \(f\) e \(g\), respectivamente. Além disso, suponha que existe uma constante \(c\) de tal forma que
\[\frac{f(t)}{g(t)} \leq c,\] para todo valor de \(t\), com \(f(t) > 0\). Para utilizar o método a aceitação e rejeição para gerar observações da v.a. \(X\), utilizando o algoritmo mais abaixo, antes, encontre uma v.a. \(Y\) com pdf ou fp \(g\), tal que satisfaça a condição acima.
Importante:
É importante que a v.a. \(Y\) escolhida seja de tal forma que você consiga gerar facilmente suas observações. Isso se deve ao fato do método da aceitação e rejeição ser computacionalmente mais intensivo que métodos mais diretos como o método da transformação ou o método da inversão que exige apenas a regração de números pseudo-aleatórios com distribuição uniforme.
Algoritmo do Método da Aceitação e Rejeição:
1 - Gere uma observação \(y\) proveniente de uma v.a. \(Y\) com fdp/fp \(g\);
2 - Gere uma observação \(u\) de uma v.a. \(U\sim \mathcal{U} (0, 1)\);
3 - Se \(u < \frac{f(y)}{cg(y)}\) aceite \(x = y\); caso contrário rejeite \(y\) como observação da v.a. \(X\) e volte ao passo 1.
Prova: Consideremos o caso discreto, ou seja, que \(X\) e \(Y\) são v.a.s com fp’s \(f\) e \(g\), respectivamente. Pelo passo 3 do algoritmo acima, temos que \(\{aceitar\} = \{x = y\} = u < \frac{f(y)}{cg(y)}\). Isto é,
\[P(aceitar | Y = y) = \frac{P(aceitar \cap \{Y = y\})}{g(y)} = \frac{P(U \leq f(y)/cg(y)) \times g(y)}{g(y)} = \frac{f(y)}{cg(y)}.\] Daí, pelo Teorema da Probabilidade Total, temos que:
\[P(aceitar) = \sum_y P(aceitar|Y=y)\times P(Y=y) = \sum_y \frac{f(y)}{cg(y)}\times g(y) = \frac{1}{c}.\] Portanto, pelo método da aceitação e rejeição aceitamos ocorrência de \(Y\) como sendo uma ocorrência de \(X\) com probabilidade \(1/c\). Além disso, pelo Teorema de Bayes, temos que
\[P(Y = y | aceitar) = \frac{P(aceitar|Y = y)\times g(y)}{P(aceitar)} = \frac{[f(y)/cg(y)] \times g(y)}{1/c} = f(y).\] O resultado logo acima, mostra que aceitar \(x = y\) pelo procedimento do algoritmo equivale a aceitar um valor proveniente de \(X\) que tem fp \(f\). Para o caso contínuo, a demonstração é similar.
Importante:
Perceba que para reduzir o custo computacional do método, deveremos escolher \(c\) de tal forma que possamos maximizar \(P(aceitar)\). Sendo assim, escolher um valor exageradamente grande da constante \(c\) irá reduzir a probabilidade de aceitar uma observação de \(Y\) como sendo observação da v.a. \(X\).
Nota:
Computacionalmente, é conveniente considerar \(Y\) como sendo uma v.a. com distribuição uniforme no suporte de \(f\), uma vez que gerar observações de uma distribuição uniforme é algo simples em qualquer computador. Para o caso discreto, considerar \(Y\) com distribuição uniforme discreta poderá ser uma boa alternativa.
Exercício
Quais as propriedades de um bom gerador de números pseudo-aleatórios? Disserte sobre cada uma delas.
Implemente o gerador Midsquare idealizado pelo matemático John von Neumann. Por que o gerador Midsquare não é um bom gerador? Explique.
Defina matematicamente o gerador congruencial linear. Implemente uma função em R que implementa esse gerador.
O gerador Randu é definido por \(x_{i + 1} = 65539 \times x_i\,\mathrm{mod}\,31\). O Randu é um gerador congruencial misto ou multiplicativo?
Por que o gerador Randu é um dos peiores geradores de números pseudo-aleatório já criado? Explique.
Defina um gerador congruencial de período completo para geração de números pseudo-aleatórios com distribuição uniforme no intervalo \((0,1)\)
Explique o método da transformação para geração de números pseudo aleatório. Apresente um exemplo.
Defina o método da inversão para geração de números pseudo-aleatórios. Sempre será possível utilizar esse método? Explique.
Implemente uma função para geração de números pseudo-aleatórios com distribuição normal padrão. A função deverá implementar o método de Box-Müller e o método polar. Ao final obtenha um histograma com os números gerados (mil valores) e realize um teste de normalidade. Realize um teste de normalidade.
Seja \(X\) uma variável aleatória em um espaço de probabilidade \((\Omega, \mathcal{A},\mathcal{P})\) e suponha que \(X \sim \mathcal{U}(0,1)\). Obtenha a distribuição de \(Y = -\log(X)\).
Com base na distribuição da variável aleatória (v.a.) \(Y\) do exercício acima, implemente uma função em R que gere observações de \(Y\).
Conhecendo a distribuição da v.a. \(X\), implemente para cada um dos itens que seguem, uma função para geração de observações da v.a. \(Y\):
\(X \sim \mathrm{Exp}(\lambda),\) com \(x \geq 0\) e \(\lambda > 0\) e \(Y = \sum_{i = 1}^n X_i \sim \Gamma(n, \lambda)\);
\(X \sim \mathrm{Exp}(\lambda)\), com \(x \geq 0\) e \(\lambda>0\) e \(Y = \mu - \beta\log(\lambda X) \sim \mathrm{Gumbel}(\mu,\beta)\), com \(\mu \in \Bbb{R}\) e \(\beta>0\);
\(X \sim \mathcal{U}(0,1)\) (contínua) e \(Y = m + s[-\log(X)]^{-1/\alpha} \sim\) Fréchet\((\alpha,s,m)\), com \(x, \alpha,s > 0\) e \(m \in \Bbb{R}\).
Cite algumas das propriedades do gerador Mersenne Twister. Qual o seu período de ocorrência?
Explique o algoritmo do método da aceitação e rejeição.
Utilizando o método da aceitação e rejeição, implemente uma função que gere valores aleatório provenientes da distribuição da v.a. \(X\) tal que
\[P(X = 1) = 0.3, P(X = 2) = 0.2, P(X = 3) = 0.35, P(X = 4) = 0.15.\]
- Implemente duas funções que geram observações da v.a. \(X\) utilizando o método da transformação para v.a. discretas e pelo método da aceitação e rejeição. Qual método é mais eficiente computacionalmente? Por que?
\[\begin{eqnarray} P(X = 0) &=& 0.14, P(X = 1) = 0.27, P(X = 2) = 0.27,\nonumber\\ P(X = 3) &=& 0.18, P(X = 4) = 0.09, P(X = 5) = 0.04, \nonumber\\ P(X = 6) &=& 0.01. \nonumber\\ \end{eqnarray}\]
Implemente a função
rdisc(n = 1L, x, probs)que retorna números pseudo-aleatórios de uma v.a. discreta \(X\) que assume uma quantidade finita de observações. Os argumentos derdiscestão especificados abaixo:n: número de observações a serem geradas;x: vetor com as possíveis observações da v.a. \(X\);probs: vetor com as probabilidades das observações passadas àx.
Implemente uma função para o método da aceitação e rejeição (
ar_fp(n, x, prob)), para o caso em que deseja-se gerar observações de uma v.a. \(X\) discreta. O argumentonrefere-se à quantidade de observações a serem geradas,xé um vetor de valores assumidos por \(X\) eprobé um vetor de probabilidades de cada observação de \(X\). A funçãoar_fp(n, x, prob)deverá escolher um valor adequado para \(c\).Seja \(X\) uma v.a. contínua com fdp \(f(x) = -6x(x-1)\), com \(0 < x < 1\). Implemente a função
rf(n, c = 1.5)que gera números pseudo-aleatórios como observações de \(X\), pelo método da aceitação e rejeição, em quené a quantidade de números a serem gerados ecé o valor da constante (0.5 por padrão) no algoritmo do método da aceitação e rejeição. Dica: considere \(Y \sim \mathcal{U}(0,1)\).
- Considerando a função
rf(n, c)implementada no exercício anterior, quantos passos serão necessários para que possamos gerar 10 mil observações proveniente da distribuição de \(X\), considerandoc = 6? Respectivamente, quantos passos serão necessários para serem gerados a mesma quantidade de observações de \(X\) considerandoc = 0.5? Dica: antes de chamar a função implementada, fixe a semente fazendoset.seed(0).
6.2 Otimização Não-Linear
Na estatísticas, em muitas situações práticas, temos o interesse de maximizar ou minimizar uma função objetivo. Por exemplo, na inferência esatística, é comum o nosso interesse na obtenção dos estimadores de máxima verossimilhança de parâmetros que indexam modelos ou distribuições de probabilidade. Um outro problema comum na estatística, mais precisamente na área de regressão é o de minimizar a soma dos quadrados de um conjunto de erros, em um modelo de regressão não-linear por meio de mínimos quadrados não-lineares.
Nota:
Aqui, o termo otimizar estará se referindo à minimiar ou maximizar uma função objetivo. Dessa forma, por meio do contexto em que o termo esteja sendo utilizado, a ideia estará implícita. Além disso, por uma simples modificação na função objetivo, um algoritmo utilizado para maximizar uma função poderá ser convertido em um algoritmo para minimização de uma função.
Suponha que temos interesse em maximizar uma função objetivo, seja ela \(\psi(\pmb{\Theta}): \pmb{\Theta} \rightarrow \mathbb{R}\), em que \(\pmb{\Theta}\) é um subspaço do \(\mathbb{R}^p\). Dessa forma, queremos encontrar o vetor \(\pmb{\theta}\) (\(p \times 1\)) que maximiza a função objetivo \(\psi(\cdot)\). Ou seja, queremos obter
\[ \underset{\pmb{\theta}\, \in\, \pmb{\Theta}}{\mathrm{arg\,max}}\,\psi(\pmb{\theta}).\]
A maioria das situações práticas nos levam à problemas com a condição de primeira ordem,
\[\frac{\partial\,\psi(\pmb{\theta})}{\partial\,\pmb{\theta}} = \pmb{0},\]
resulta em um sistema de equações não-lineares que não apresenta solução em forma fechada. Nesses casos, a solução do problema de minimizar \(\psi(\pmb{\theta})\) é obtida utilizando-se de métodos/algoritmos iterativos.
6.2.1 Metódos Gradiente
A classe de métodos de otimizações mais utilizadas em situações em que a condição de primeira ordem resulta em um sistema não-linear que não possue forma fechada é denominada de classe de métodos gradiente. Nessa classe de métodos, a atualização de \(\pmb{\theta}\) para um vetor que mais se aproxima do ponto que minimiza \(\psi(\cdot)\) (função objetivo) é dada de forma iterativa. Dessa forma, seja \(\pmb{\theta}_0\) o ponto inicial (chute inicial) na \(t\)-ésima iteração. Se o valor de \(\pmb{\theta}\) que maximiza globalmente a função \(\psi(\cdot)\) não tiver sido alcançado, calcula-se o vetor direcional (vetor gradiente) de \(\psi(\cdot)\), denotado aqui por \(\pmb\Delta_t\) (\(p \times 1\)) e o “tamanho do passo” \(\lambda_t\). Assim, o próximo valor de \(\pmb\theta\) será atualizado para:
\[\pmb\theta_{t+1} = \pmb\theta_t + \lambda_t \pmb \Delta_t.\]
Importante:
O vetor gradiente fornece a direção e o sentido de deslocamento, apartir de um ponto especificado, de subida que fornece um incremento em uma grandeza. No nosso caso, \(\pmb\Delta_t\) (\(p \times 1\)) irá indicar o sentido de subida, em que poderemos atualizar o valor de \(\pmb \theta\) para um ponto que maximiza \(\psi(\cdot)\). Dessa forma, \(-\pmb\Delta_t\) fornecerá a direção e o sentido de atualização de \(\pmb\theta\) que nos levam à pontos que minimizam \(\psi(\cdot)\).
Note também que, em cada iteração do algoritmo, temos que \(\pmb \theta_t\) e \(\pmb \Delta_t\) são conhecidos, uma vez que \(\pmb \theta_t\) é o ponto \(\pmb \theta\) atualizado na iteração \(t-1\) e \(\pmb \Delta_t\) é o vetor gradiente da função objetivo avaliado em \(\pmb \theta_t\).
Dado o conhecimento dessas quantidade, perceba que precisamos obter o “tamanho do passo” \(\lambda_t\). Assim, iremos recair em um problema de otimização secundário, denominado de procura em linha. Sendo assim, busca-se \(\lambda_t\) de tal forma que
\[\frac{\partial \pmb\,\psi(\pmb \theta_t + \lambda_t\pmb\Delta_t)}{\partial \lambda_t} = \delta(\pmb \theta_t + \lambda_t\pmb\Delta_t)^{'}\pmb \Delta_t = 0,\] em que \(\delta(\pmb \theta_t + \lambda_t\pmb\Delta_t)^{'}\) é o vetor gradiente transposto (\(1 \times p\)) da função objetivo avaliado no ponto \(\pmb \theta_t + \lambda_t\pmb\Delta_t.\)
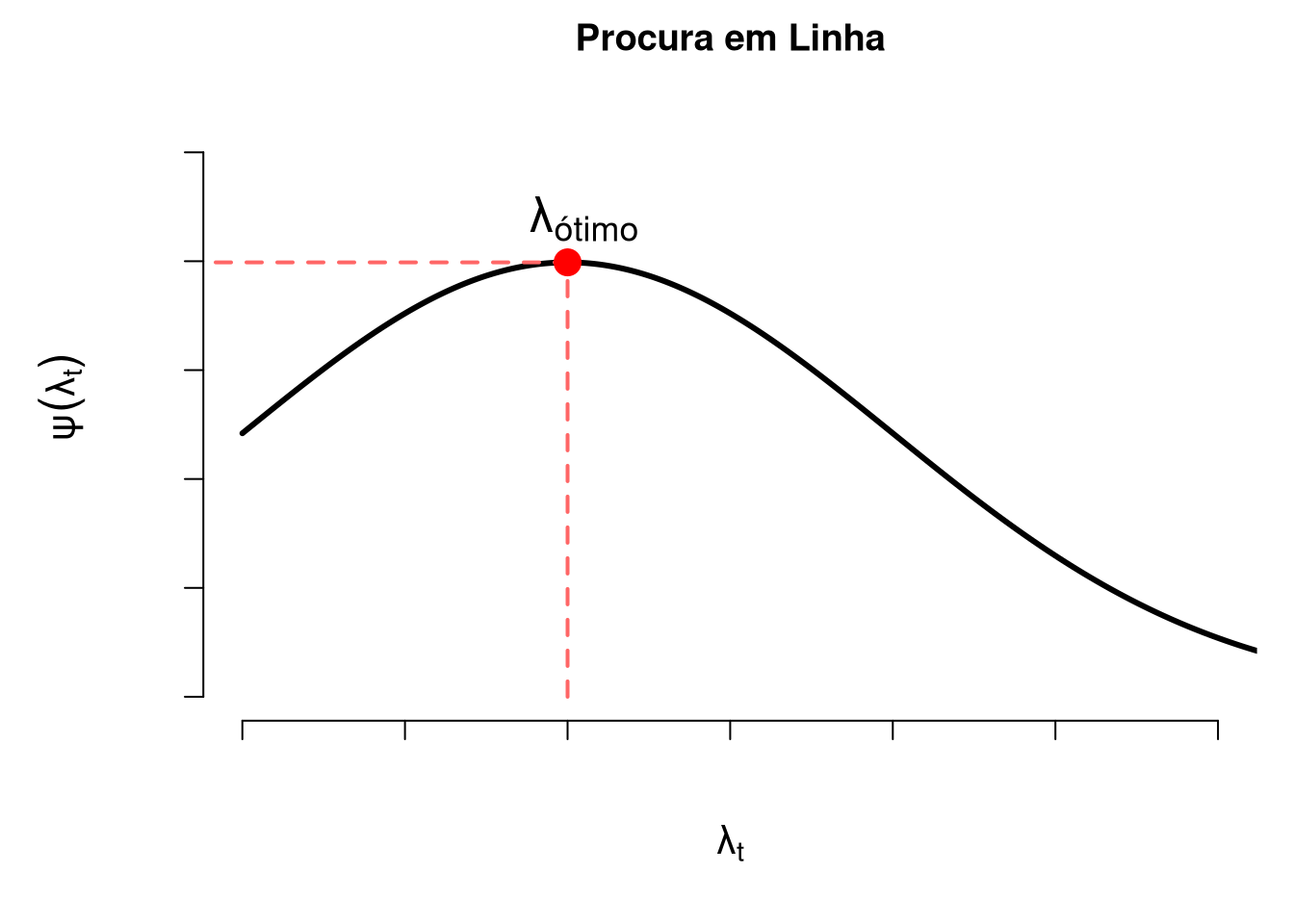
Figura 6.1: Poblema de procura em linha, em que a função objetivo é função penas do tamanho do passo.
Observação:
É importante observar que o processo de busca em linha em um algoritmo de otimização não-linear tornará esse algoritmo computacionalmente intensivo. Dessa forma, muitos algoritmos adotam um conjunto de regras ad hoc que são computacionalmente menos custosas. Essa classe de algoritmos é o que denominamos de classe de métodos gradiente.
Na classe de métodos gradiente, fazemos
\[\pmb \Delta_t = M_t\delta_t,\] em que \(M_t\) (\(p \times p\)) é uma matriz positiva-definida e \(\delta_t\) (\(p \times 1\)) é o gradiente de \(\pmb\psi\), ambos na \(t\)-ésima iteração. Para deixar claro, temos que \(\delta_t\) = \(\delta_t(\pmb \theta_t) = \partial \, \psi(\pmb \theta_t)/\partial\, \pmb \theta_t\).
A motivação por trás dos métodos gradientes em tomar \(\pmb \Delta_t = M_t\delta_t\) poderá ser entendida ao considerar uma aproximação para \(\psi(\pmb \theta_t + \lambda_t\pmb\Delta_t)\) por uma série de Taylor de primeira ordem, em torno do ponto \(\lambda_t = 0\). Assim, temos que,
\[\psi(\pmb \theta_t + \lambda_t\pmb\Delta_t) \approx \psi(\pmb \theta_t) + \lambda_t \delta_t^{'}\pmb \Delta_t,\] em que \(\delta_t^{'}\) é o vetor gradiente transposto (\(1 \times p\)). Para reduzir a notação, tome \(\psi(\pmb \theta_t + \lambda_t\pmb\Delta_t) = \psi_{t+1}\). Assim, temos que
\[\psi_{t+1} - \psi_{t} \approx \lambda_t \delta_t^{'}\pmb \Delta_t.\]
Assim, considerando \(\pmb \Delta_t = M_t\delta_t\), temos que
\[\psi_{t+1} - \psi_{t} \approx \lambda_t \delta_t^{'}M_t\delta_t.\]
Para \(\delta_t\) diferente de zero e \(\lambda_t\) suficientemente pequeno, se \(\psi(\pmb\theta)\) não assume o valor máximo da função, podemos sempre encontrar um tamanho de passo tal que uma iteração adicional no algoritmo irá incrementar o valor da função, ou seja, se aproximará um pouco mais do máximo global da função objetivo.
Perceba que sempre temos que \(\psi_{t+1} - \psi_{t} \geq 0\). Isso sempre será verdade, uma vez que \(M_t\) é uma matriz positiva-definida, o que implica que \(\delta_t^{'}M_t\delta_t > 0\). Além disso, na situação de \(\psi(\pmb\theta)\) não encontar-se no ponto máximo, como mencionado no parágrafo anterior, sempre haverá um tamanho de passo \(\lambda_t\), por menor que ele seja.
6.2.1.1 Steepest Ascent
O algoritmo steepest ascent (“subida mais inclinada”) é o mais simples dos métodos gradientes. A ideia do algoritmo steepest ascent é considerar
\[M_t = I,\] em que \(I\) é a matriz identidade (\(p \times p\)). Dessa forma, temos que \(\pmb \Delta_t = \delta_t\), em todos os passos iterativos. Daí, a atualização de \(\pmb \theta\) é dada por:
\[\pmb \theta_{t+1} = \theta + \lambda_t\delta_t.\]
Nota:
Esse algoritmo tende a ser pouco utilizado na prática, uma vez que apresenta convergência lenta. Esse método é muito semelhante ao algoritmo gradiente descendente steepest descent, utilizado para minimização. Não confunda steepest descent citado aqui com um método de aproximação de integrais que leva o mesmo nome.
6.2.1.2 Newton-Raphson
O método de Newton-Raphson, muitas vezes apenas chamado de método de Newton, considera a atualização de \(\pmb \theta\) na forma
\[\pmb \theta_{t+1} = \pmb \theta_t -H_t^{-1}\delta_t,\] em que
\[H = H(\theta) = \frac{\partial^2 \psi(\pmb \theta)}{\partial \pmb \theta \partial \pmb \theta^{'}},\] ou seja, temos que \(H\) é a matriz hessiana. No método de Newton-Rapshon, temos que \(\lambda_t = 1\) e \(M_t = -H_t^{-1}\), em todas iterações.
Observação:
A matriz hessiana nos permite identificar a concavidade de uma função multiparamétrica, desde que estas sejam duplamente diferenciável. Em um problema de maximização de uma função objetivo, temos que a matriz hessiana é negativa definida em uma região muito próxima ao ponto que maximiza a função. Dessa forma, \(-H^{-1}\) é uma matriz positiva definida na mesma região, isto é, se \(\pmb a\) é um vetor qualquer (\(p \times 1\)) e \(H^{-1}\) é uma matriz (\(p \times p\)), então \(-\pmb a^{'} H^{-1} \pmb a < 0\).
Seja \(H\) uma matriz hessiana como apresentada acima. Abaixo estão listadas algumas propriedades da de \(H\). Dessa forma, Então
\(\pmb a^{'} H \pmb a > 0\) (positiva-definida): A função é estritamente convexa;
\(\pmb a^{'} H \pmb a < 0\) (negativa-definida): A função é estritiamente concava. Essa é a propriedade que estamos considerando, visto que estamos em um problema de maximização de uma função objetivo;
\(\pmb a^{'} H \pmb a \geq 0\) (positiva semidefinida): A função é parcialmente convexa;
\(\pmb a^{'} H \pmb a \leq 0\) (negativa semidefinida): A função é parcialmente concava;
\(H\) é uma matriz simétrica;
A inversa de uma matriz positiva-definida é também uma matriz positiva-definida;
Você poderá entender a matriz hessiana como a primeira derivada do vetor gradiente da função objetivo.
O método de Newton-Raphson normalmente é utilizado para encontar os zeros de uma função. Quando aplicado sobre a condição de primeira ordem, o método de Newton-Raphson nos conduzirá aos pontos críticos da função. Como fazemos uso do vetor gradiente, estaremos sempre a caminhar para os pontos de máximo de \(\psi(\cdot)\). Dessa forma, os pontos críticos são os pontos de máximo da função objetivo.
Para que possamos entender melhor a ideia do método, considere uma expansão de Taylor da condição de primeira ordem em torno de um ponto qualquer \(\pmb \theta_0\). Assim, temos que
\[\frac{\partial\,\psi(\pmb \theta)}{\partial\, \pmb \theta} \approx f(\pmb \theta_0) + H(\pmb \theta_0) (\pmb \theta - \pmb\theta_0).\]
Resolvendo o sistema para \(\pmb\theta\) e fazendo \(\pmb \theta = \pmb \theta_{t+1}\) e \(\pmb \theta_0 = \pmb \theta_t\), obteremos o esquema iterativo do algoritmo apresentado ascima.
A forma mais usual do algoritmo de Newton-Rapshon introduz o mecanismo de “procura em linha.” Dessa forma, o esquema iterativo é dada por
\[\pmb \theta_{t+1} = \pmb \theta_t -\lambda_tH_t^{-1}\delta_t.\] Nota:
O método de Newton-Raphson apesar de funcionar bem em diversas situações, poderá fornecer estimativas ruins em alguns casos. Por exemplo, um problema comum é quando \(\pmb \theta_t\) é um ponto distante do ponto que maximiza \(\psi(\cdot)\), uma vez que nesses pontos, a matriz \(M_t = -H^{-1}\) pode não ser positiva-definida.
6.2.1.3 BHHH
O método BHHH (Berndt-Hall-Hall-Hausman), foi proposto no artigo Berndt, E. R., Hall, B. H., Hall, R. E., & Hausman, J. A. (1974). Estimation and inference in nonlinear structural models. In Annals of Economic and Social Measurement, Volume 3, p. 653-665. O método é muito semelhante ao método de Newton-Raphson, com a diferença que trocamos a matriz \(H_t\) pelo auto produto dos vetores gradientes \(\delta_t\delta_t^{'}\)
Nota:
A vantagem do método BHHH está no fato de não necessitarmos calcular segundas derivadas. Trata-se de um método muito utilizado em aplicações ecnonométricas. O método BHHH poderá enfrentar o mesmo problema de convergência que o método de Newton-Raphson.
6.2.1.4 Métodos quasi-Newton
A classe de algoritmos quasi-Newton é composta por algoritmos que são bastante eficientes do ponto de vista de convergência e também do ponto de vista computacional, visto que esses algoritmos não requerem o cálculo de segundas derivadas. Nessa classe de algoritmos, é utilizado uma sequência de matrizes tal que
\[M_{t+1} = M_{t} + N_t,\] sendo \(N_t\) uma matriz positiva-definida. Assim, se \(M_0\) é positiva-definida, \(M_t\) na \(t\)-ésima iteração sempre será positiva-definida. A ideia básica desses métodos é construir uma aproximação para \(-H(\pmb \theta)^{-1}\), de tal forma que
\[\lim_{t \to \infty} M_t = -H^{-1}.\]
Há diversos algoritmos que pertencem à classe de métodos quasi-Newton. Por exemplo, o método DFP (Davidon, Fletcher e Powell) atualiza \(M_{t+1}\) fazendo
\[M_{t+1} = M_{t} + \frac{\pmb \gamma_t \pmb \gamma_t^{'}}{\pmb \gamma_t^{'}\kappa_t} + \frac{M_t\kappa_t\kappa_t^{'}M_t}{\kappa_t^{'}M_t\pmb \gamma_t},\]
em que \(\pmb \gamma_t = \pmb \theta_{t+1} - \pmb \theta_t\) (diferença de pontos) e \(\kappa_t = \delta(\pmb \theta_{t+1}) - \delta(\pmb \theta_t)\) (diferenças de gradientes avaliados em pontos).
O algoritmo quasi-Newton mais utilizado é o BFGS (Broyden-Fletcher-Goldfarb-Shanno). O algoritmo BFGS tem a atualização semelhante ao DFP, com a diferença que é subtraído o termo \(a_tb_tb_t^{'}\), em que \(a_t = \kappa_t^{'}M_t\kappa_t\) e
\[b_t = \frac{\pmb\gamma_t}{\pmb\gamma_t^{'}\kappa_t} - \frac{M_t\kappa_t}{\kappa_t^{'}M_t \kappa_t}.\]
Sendo assim, temos que no método BFGS, a atualização de \(M_t\) de dará por:
\[M_{t+1} = M_{t} + \frac{\pmb \gamma_t \pmb \gamma_t^{'}}{\pmb \gamma_t^{'}\kappa_t} + \frac{M_t\kappa_t\kappa_t^{'}M_t}{\kappa_t^{'}M_t\pmb \gamma_t} - a_tb_tb_t^{'}.\]
Nota:
O termo quasi-Newton é empregado para se referir ao fato de que esses métodos não fazem uso da matriz hessiana. Porém, esses métodos utilizam uma aproximação iterativa de uma matriz \(M_t\) que converge para a matriz de segundas derivadas. Dessa forma, não entenda o termo quasi-Newton como se esses métodos fossem inferiores aos métodos de Newton-Raphson. Na verdade, os métodos quasi-Newton normalmente apresentam desempenho superior.
6.3 Otimização não-linear no R
Em R, é comum minimizar uma função objetivo utilizando a função optim() do pacote stats que está disponível em qualquer instalação básica da linguagem. A forma geral de uso da função optim() é:
optim(par, fn, gr = NULL, ...,
method = c("Nelder-Mead", "BFGS", "CG", "L-BFGS-B", "SANN",
"Brent"),
lower = -Inf, upper = Inf,
hessian = FALSE)em que:
paré um vetor de chutes inicias;fné a função objetivo a ser minimizada;gré a função gradiente da funçãofn;methodé o método escolhido par minimizarfn. É possível escolher os métodos de Nelder-Mead, BFGS, CG, L-BFGS-B, SANN (Simulated Annealing) e Brent;...é o operador dot-dot-dot que poderá receber argumentos que por ventura possam existir nas funçõesfnegr;loweré um vetor que limita inferiormente os parâmetros a serem otimizados (por padrão é-Inf);upperé um vetor que limita superiormente os parâmetros a serem otimizados (por padrão éInf);hessianrecebe um valor lógico, em que por padrãohessian = FALSE. Sehessian = TRUE, será calculado uma estimativa da matriz hessiana avaliada na estimativa de ponto de mínimo global.
Exemplo: Utilizando a função optim() para minimizar a função Rosenbrock pelo método BFGS.
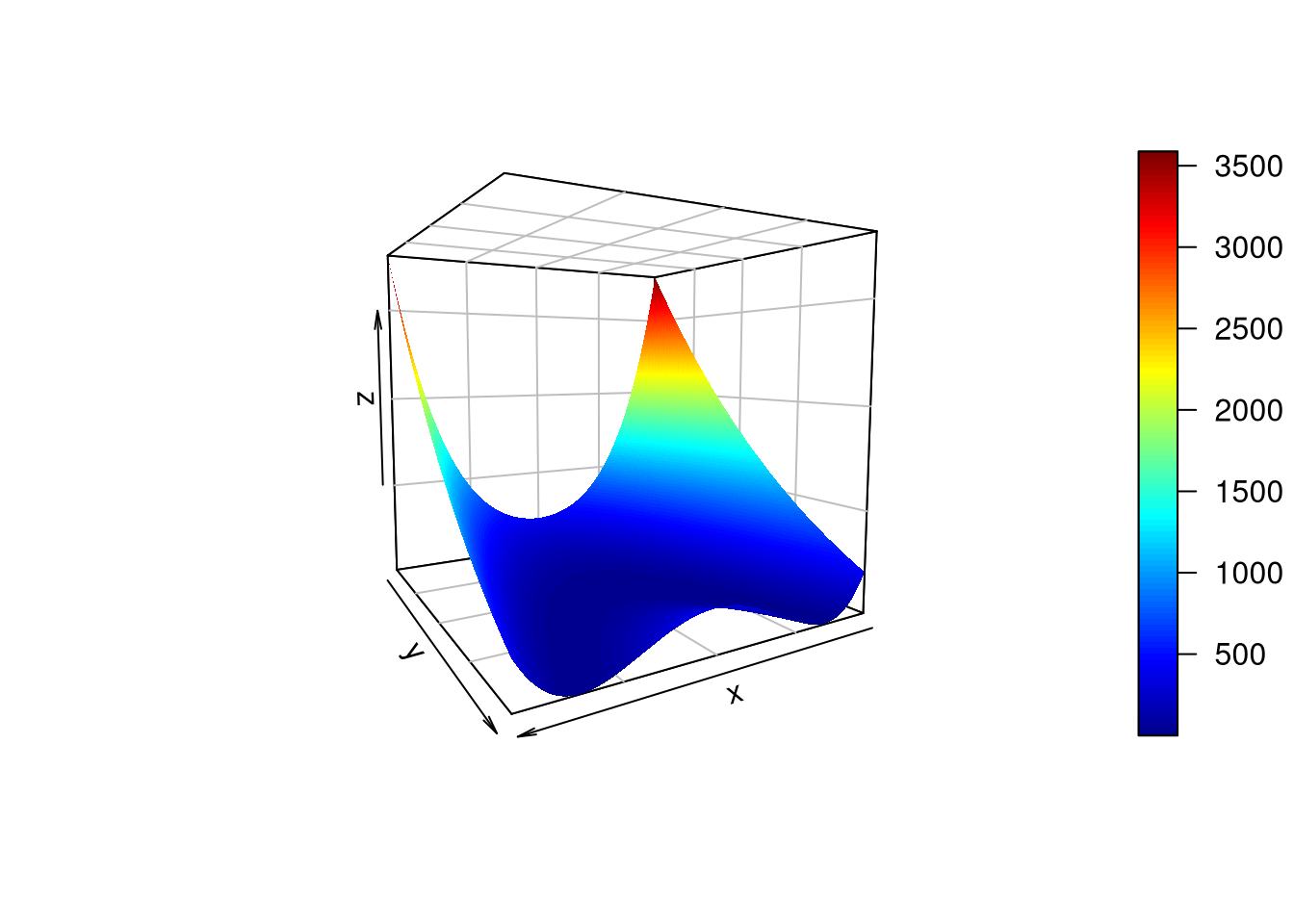
Figura 6.2: Gráfico da superfície da função Rosenbrock introduzida por Howard H. Rosenbrock em 1960.
# Função Rosenbrock
f_objetivo <- function(x, a = 2, b = 40) {
x1 <- x[1]
x2 <- x[2]
(a - x1) ^ 2 + b * (x2 - x1 ^ 2) ^ 2
}
optim(par = c(2, 2), fn = f_objetivo, method = "BFGS")## $par
## [1] 1.999998 3.999992
##
## $value
## [1] 2.761362e-11
##
## $counts
## function gradient
## 128 45
##
## $convergence
## [1] 0
##
## $message
## NULLEntendendo a saída (retorno da função):
paré um vetor contendo as estimativas para \(x_1\) e \(x_2\);valueé o valor da função avaliada nas estimativas obtidas;countsé a quantidade de chamadas da função a ser otimizada e do seu gradiente. Note que não passamos o gradiente da função de objetivo mas este teve que ser calculado numericamente;convergenceé um vetor de uma única posição, em que 0 indica convergência. Qualquer número diferente de zero indica que houve problema de convergência no algoritmo escolhido para mininizar a função objetivo;messageretorna alguma mensagem com informações adicionais, se necessário. Caso contrário,NULLserá o retorno.
A função de Rosenbrock tem mínimo analítico no ponto \((a, a^2)\) (ponto ótimo), em que \(f(a, a^2) = 0\). Dessa forma, um bom método de otimização nos trará uma estimativa próxima ao ponto \((2, 4)\), uma vez que foi considerado, no código acima, \(a = 2\) e \(b = 40\). Como pode-se observar, o método BFGS forneceu uma boa estimativa para ponto ótimo analítico.
Nota:
Para o exemplo acima, \(x_1\) e \(x_2\) são chamadas de variáveis, visto que a função de Rosenbrock é determinística. Porém, em problemas estatísticos, por exemplo, quando desejamos maximizar uma função de log-verossimilhança, a otimização é realizada em termos dos parâmetros que indexam o modelo estatístico. Nesse caso, cada ponto da função
O argumento ... é muito importante para nós que necessitamos frequentemente maximizar uma função de log-vessimilhança \(\mathcal{l}(\pmb \theta)\). É por meio desse argumento que passamos a amostra para \(\mathcal{l}(\pmb \theta)\). Sem ele, teríamos que implementa uma função de verossimilhança para cada tamanho de amostra, o que seria impraticável. Com a amostra especificada, poderemos proceder a minimização de \(-\mathcal{l}(\pmb \theta)\) e obter o vetor \(\pmb \theta\) com as estimativas de máxima verossimilhança dos parâmetros que indexam um modelo probablístico.
Exemplo: Considere o conjunto de dados obtido abaixo:
set.seed(0L)
dados <- rnorm(n = 750L, mean = 2, sd = 1)Seja \(X_1, \ldots, X_n\) uma amostra aleatória (v.a.’s i.i.d), em que \(X_i \sim \mathcal{N}(\mu = 2, \sigma^2 = 1)\, \forall i\). Obtenha pelo método BFGS os estimadores de máxima verossimilhança para \(\mu\) e \(\sigma^2\). Seja \(\mathcal{l(\pmb\theta)}\) a função de verossimilhança para amostra e \(\pmb \theta^{'} = (\mu, \sigma^2)\). Precisaremos implementar a função de verossmilhança e multiplica-la por -1, uma vez que minimizando \(-\mathcal{l}(\pmb \theta)\) equivale à maximizar \(\mathcal{l}(\pmb \theta)\).
set.seed(0L)
dados <- rnorm(n = 750L, mean = 2, sd = 1)
# Função de log-verssimilhança da amostra aleatória.
loglikelihood_normal <- function(par, x){
mu <- par[1]
sigma2 <- par[2]
-sum(log(dnorm(x, mean = mu, sd = sqrt(sigma2))))
}
# maximizando -log-likelihood da amostra aleatória.
resultado <- optim(par = c(1, 1), fn = loglikelihood_normal,
method = "BFGS", x = dados)
# Graficando a densidade estimada sobre os dados ----------------------------------
# Sequência no domínio da distribuição:
x <- seq(-5, 6, length.out = 1000L)
y <- dnorm(x = x, mean = resultado$par[1], resultado$par[2])
# Histograma das observações:
hist(x = dados, main = "Função Densidade de Probabilidade Estimada",
ylab = "Probabilidade", xlab = "x", probability = TRUE,
col = rgb(1, 0.9, 0.8), border = NA)
# Tracejando a densidade sobre o histograma:
lines(x, y, lwd = 2)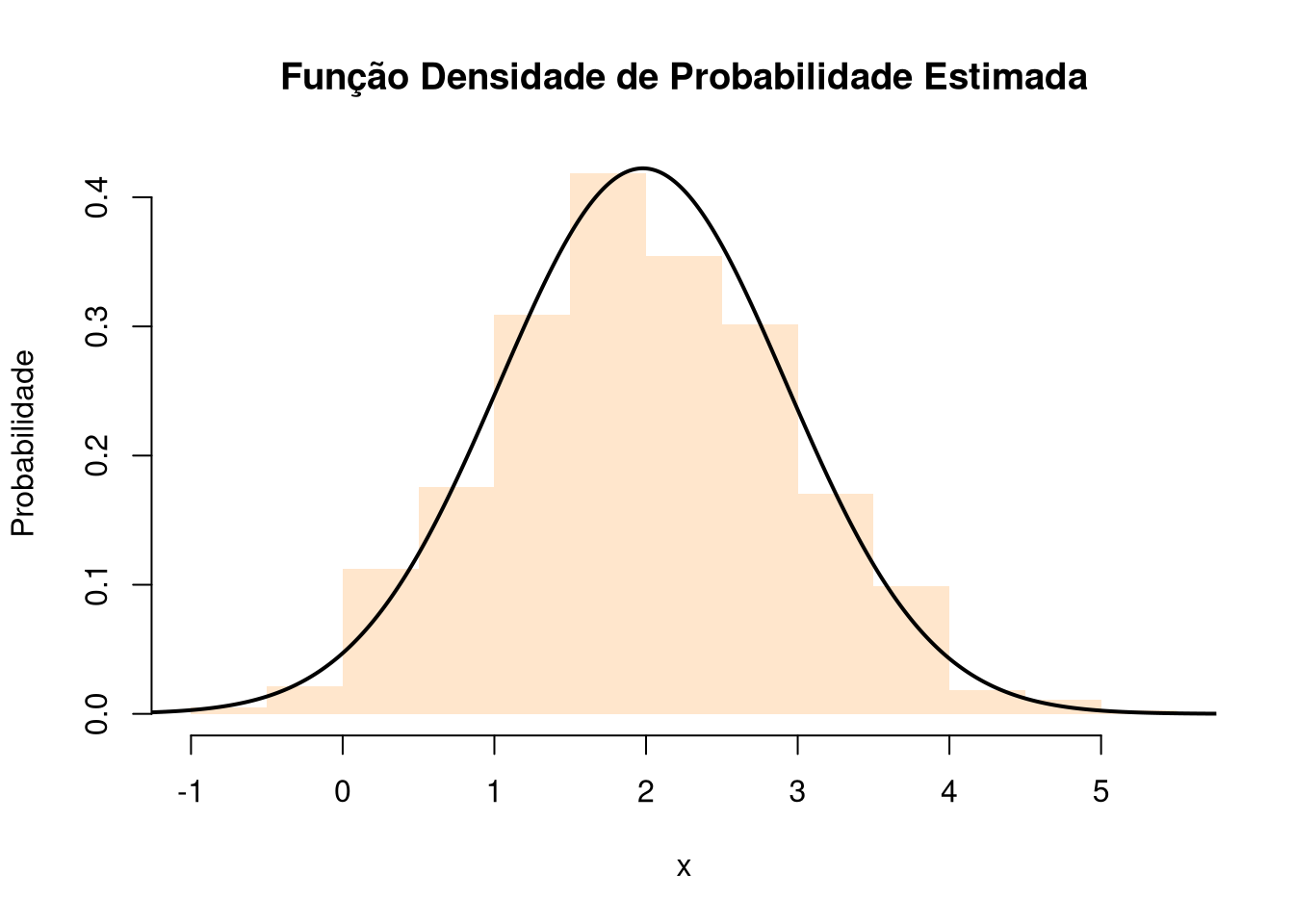
Importante:
Nunca esqueça que minimizar \(-f\) é equivalente a maximizar \(f\), sendo tabém verdadeira a recíproca. Além disso, lembre-se também que a função optim() é implementada de forma a minimizar uma função objetivo.
Exercício
Defina matematicamente o método gradiente para maximização de uma função \(\psi(\pmb{\theta}): \pmb{\Theta} \rightarrow \mathbb{R}\), em que \(\pmb{\Theta}\) é um subespaço do \(\mathbb{R}^p\).
Qual a desvantagem do uso do processo de busca em linha em algoritmos de otimização não-linear?
Defina os métodos quasi-Newton e o que os diferenciam dos de Newton? Qual as vantagens que a maioria desses métodos apresentam com relação aos métodos de Newton?
Enuncie os métodos Steepest Ascent, Newton-Raphson e BHHH. Esses são métodos de Newton ou quasi-Newton? Explique.
Considere a função abaixo:
\[f(\theta) = 6 + \theta ^ 2 \times \sin(14\theta),\] em que \(-2.5 \leq \theta \leq 2.5\). Obtenha uma estimativa para o ponto de máximo global dessa função. Houve convergência? Explique. Além disso, construa um gráfico da função \(f(\theta)\) destacando o ponto de máximo no gráfico da função.
Considere a Matyas function, função definida logo abaixo:
\[f(x, y) = 0.26 \times (x^2 + y^2) - 0.48 \times xy,\] em que \(0 \leq x, y ,\leq 10\). Qual o ponto de mínimo global da função? Obtenha uma estimativa, utilizando o método BFGS, para o ponto de mínimo global da função. Além disso, construa o gráfico da superfície obtida pela função e o gráfico com as curvas de níveis da função com a estimativa obtida indicada como um ponto nesse último gráfico. Interprete o resultado obtido. Houve convergência?
Considere a Himmelblau’s function, função definida por:
\[f(x, y) = (x^2 + y -11)^2 + (x + y^2 - 7)^2,\]
com \(-5 \leq x,y \leq 5\). Essa função possui quatro pontos de mínimo global, são eles:
\[ \mathrm{Min} = \left \{ \begin{array}{rcc} f(3.0, 2.0) & = & 0.0 \\ f(-2.805118, 3.131312) & = & 0.0 \\ f(-3.779310, -3.283186) & = & 0.0 \\ f(3.584428, -1.848126) & = & 0.0 \end{array} \right. \] Obtenha uma estimativa, utilizando o método BFGS, para o ponto de mínimo global da função. Além disso, construa o gráfico da superfície obtida pela função e o gráfico com as curvas de níveis da função com a estimativa obtida indicada como um ponto nesse último gráfico. Interprete o resultado obtido. Houve convergência?
Considere a Earson function, função definida abaixo:
\[f(x,y) = -\cos(x)\cos(y)\exp\{-[(x-\pi)^2 + (y-\pi)^2]\},\]
em que \(-100 \leq x,y \leq 100\). Essa função possui mínimo global no ponto \((\pi,\pi)\), com \(f(\pi,\pi) = -1\). Obtenha uma estimativa, utilizando o método BFGS, para o ponto de mínimo global da função. Além disso, construa o gráfico da superfície obtida pela função e o gráfico com as curvas de níveis da função com a estimativa obtida indicada como um ponto nesse último gráfico. Interprete o resultado obtido. Houve convergência? O que você observa variando os chutes iniciais?
Por que os métodos de Newton ou quasi-Newton apresentam dificuldades de otmizar uma função objetivo como a função do exercício logo acima? Explique.
Considere Hölder table function, função definida como:
\[f(x,y) = - \left| \sin(x) \cos(y) \exp \left( \left| 1 - \frac{\sqrt{x^2 + y^2}}{\pi} \right| \right) \right|,\] em que \(-10 \leq x,y \leq 10\). Essa função possui mínimos globais em:
\[ \mathrm{Min} = \left\{ \begin{array}{ccc} f(8.05502,\, 9.66459) & = & -19.2085 \\ f(-8.05502,\, 9.66459) & = & -19.2085 \\ f(8.05502,\, -9.66459) & = & -19.2085 \\ f(-8.05502,\,-9.66459) & = & -19.2085 \\ \end{array} \right. \] Obtenha uma estimativa, utilizando o método BFGS, para o ponto de mínimo global da função. Além disso, construa o gráfico da superfície obtida pela função e o gráfico com as curvas de níveis da função com a estimativa obtida indicada como um ponto nesse último gráfico. Interprete o resultado obtido. Houve convergência?
Considere a Eggholder function, função definida como:
\[f(x,y) = -(y + 47)\sin \left(\sqrt{\left|\frac{x}{2} + (y + 47)\right|}\right) - x\sin(\left|x - (y + 47)\right|),\] em que \(-512\leq x,y \leq 512\). Essa função possui mínimo global no ponto \((512, 404.2319)\), assumiando o valor mínio, nesse ponto, em \(-959.6407\). Obtenha uma estimativa, utilizando o método BFGS, para o ponto de mínimo global. Além disso, construa o gráfico da superfície e o gráfico com as curvas de níveis, em que este último deverá apresentar o ponto da estimativa obtida. Houve convergência?
Nadarajah e Haghighi (2011) propuseram a distribuição de probabilidade Nadarajah-Haghighi (NH), em que se \(X\) é uma v.a. tal que \(X \sim \mathrm{NH}(\alpha, \lambda)\), então a f.d.p. da v.a. \(X\) é dada por:
\[f_X(x) = \alpha \lambda (1 + \lambda x)^{\alpha - 1}\exp\{1 - (1 + \lambda x)^\alpha\},\] com \(x > 0\) e \(\alpha, \lambda > 0\). Perceba para \(\alpha = 1\), obtemos a f.d.p. de uma v.a. com distribuição exponencial com parâmetro \(\lambda\). Considere o conjunto de dados: 1.7, 2.2, 14.4, 1.1, 0.4, 20.6, 5.3, 0.7, 1.9, 13.0, 12.0, 9.3, 1.4, 18.7, 8.5, 25.5, 11.6, 14.1, 22.1, 1.1, 2.5, 14.4, 1.7, 37.6, 0.6, 2.2, 39.0, 0.3, 15.0, 11.0, 7.3, 22.9, 1.7, 0.1, 1.1, 0.6, 9.0, 1.7, 7.0, 20.1, 0.4, 2.8, 14.1, 9.9, 10.4, 10.7, 30.0, 3.6, 5.6, 30.8, 13.3, 4.2, 25.5, 3.4, 11.9, 21.5, 27.6, 36.4, 2.7, 64.0, 1.5, 2.5, 27.4, 1.0, 27.1, 20.2, 16.8, 5.3, 9.7, 27.5, 2.5, 27.0. 1 - Obtenha as estimativas de máxima verossimilhança, pelo método BFGS, para os parâmetros \(\alpha\) e \(\lambda\) que indexam \(f_X(x)\). 2 - Construa o histograma dos dados e sobreponha a f.d.p. estimada sobre o histograma. 3 - A densidade estimada parece ajusta-se bem ao conjunto de dados? 4 - Houve convergência do método BFGS? 5 - Em caso de haver convergência, ela é suficiente para garantir de a \(f_X(x)\) irá modelar o conjunto de dados? Explique.
Refaça o exercício acima considerando o conjunto de dados: 0.08, 2.09, 3.48, 4.87, 6.94, 8.66, 13.11, 23.63, 0.20, 2.23, 3.52, 4.98, 6.97, 9.02, 13.29, 0.40, 2.26, 3.57, 5.06, 7.09, 9.22, 13.80, 25.74, 0.50, 2.46, 3.64, 5.09, 7.26, 9.47, 14.24, 25.82, 0.51, 2.54, 3.70, 5.17, 7.28, 9.74, 14.76, 26.31, 0.81, 2.62, 3.82, 5.32, 7.32, 10.06, 14.77, 32.15, 2.64, 3.88, 5.32, 7.39, 10.34, 14.83, 34.26, 0.90, 2.69, 4.18, 5.34, 7.59, 10.66, 15.96, 36.66, 1.05, 2.69, 4.23, 5.41, 7.62, 10.75, 16.62, 43.01, 1.19, 2.75, 4.26, 5.41, 7.63, 17.12, 46.12, 1.26, 2.83, 4.33, 5.49, 7.66, 11.25, 17.14, 79.05, 1.35, 2.87, 5.62, 7.87, 11.64, 17.36, 1.40, 3.02, 4.34, 5.71, 7.93, 11.79, 18.10, 1.46, 4.40, 5.85, 8.26, 11.98, 19.13, 1.76, 3.25, 4.50, 6.25, 8.37, 12.02, 2.02, 3.31, 4.51, 6.54, 8.53, 12.03, 20.28, 2.02, 3.36, 6.76, 12.07, 21.73, 2.07, 3.36, 6.93, 8.65, 12.63, 22.69.
6.4 Monte Carlo
6.4.1 Um breve histórico
Os métodos de Monte Carlo (MC) é uma classe de metodologias bastante utilizada na estatística moderna. De um modo geral, tais metodologias calculam quantidades sob amostras aleatórias que são gerada/obtidas de forma iterativa, em que ao final obtem-se estatísticas de interesse com base nos resultados armazenados. Os métodos de MC, por exemplo, poderão ser utilizado para estimar parâmetros da distribuição amostral de uma estatística e para o cálculo do erro quadrático médio (EQM). Estudos de MC podem ser projetados para avaliar a probabilidade de cobertura de um intervalo aleatório (probabilidade do intervalo conter o parâmetro verdadeiro) ou para avaliação do Erro Tipo I em um procedimento de teste de hipóteses. Esses são apenas alguns exemplo do uso dos métodos de MC.
Os métodos de MC auxiliam os estatísticos no processo de compararem modelos/estatísticas, em que cada um(a) desses modelos/estatísticas serão submetidos à amostras com “características” prefixadas. Normalmente essas comparações serão realizadas em situações em que evidências analíticas não são possíveis de serem obtidas devido à complexidade dos modelos/estatísticas envolvidas. Sendo assim, ao utilizar-se um procedimento de MC, torna-se desnecessário escrever as equações diferenciais que descrevem o comportamento de um sistema complexo.
Além da estatística, os métodos de MC são bastante utilizados por profissionais em campos díspares como finanças, engenheria, física, biologia, entre outros.
Nota:
Para implementar um método de MC é necessário ter uma fonte de geração de números pseudo-aleatórios além da capacidade de controlarmos a sequência de números gerados. No R, como vimos anteriormente, teremos a nossa disposição diversas funções para a geração de números pseudo-aleatórios uniforme e não-uniformes e poderemos controlar a sequência gerada utilizando a função set.seed().
De acordo com Hammersley, no livro Monte Carlo Methods, 1964, o nome “Monte Carlo” surgiu durante o projeto Manhattan na época da Segunda Guerra Mundial. O Projeto Manhattan foi liderado pelos Estados Unidos com o apoio do Reino Unido e Canadá e tinha como objetivo desenvolver pesquisas para a produção das primeiras bombas atômicas durante o período de guerra. A pesquisa foi uma das maiores colaborações científicas já realizadas e deu origem a inúmeras novas tecnologias, indo muito além do aproveitamente da fissão nuclear.

Figura 6.3: Primeiro teste nuclear (nome de código Trinity), uma das três bombas atômicas produzidas pelo Projeto Manhattan. Teste realizado em 16 de julho de 1945. Com apenas 0.025 segundos após a detonação, o impacto já tomava conta de uma região com 100 metros de diâmetro.
O Projeto Manhattan foi conduzido no Laboratório Nacional de Los Alamos, construído para desenvolver as primeiras bombas atômicas utilizadas na Segunda Guerra Mundial. À época, tratava-se de um centro secreto das forças aliadas para o desenvolvimento de armas nucleares conhecido por Site Y. Atualmente o laboratório trata-se de uma das maiores instituições científicas multidisciplinares.

Figura 6.4: Laboratório de Los Alamos, laboratório federal pertencente ao Departamento de Energia dos Estados Unidos (DOE), gerido pela Universidade da Califórnia, localizado em Los Alamos, Novo México.
O Laboratório Nacional de Los Alamos, em toda sua história, reuniu diversos cientistas catedráticos e ganhadores de prêmios importantes como, por exemplo, o Prêmio Nobel. Na época da Segunda Guerra, diversos cientisticas de grande importância para o desenvolvimento científico e tecnológico atual faziam parte do projeto como Stanislaw Ulam, Richard Feynman e John von Neumann.

Figura 6.5: John von Neumann, Richard Feynman e Stanislaus Ulam em Los Alamos durante o Projeto Manhattan (da direita para a esquerda).
No ano de 1946, enquanto se recuperava de uma encefalite, o matemático Stanislaw Ulam jovava paciência. Ele tentou calcular as probabilidades de alguns eventos no jogo utilizando análise combinatória. Porém, percebeu que uma alternativa mais prática seria realizar inúmeras jogadas e contar quantas vezes cada resultado ocorria, ou seja, utilizar a teoria frequentista de probabilidade. Detalhes sobre essa história poderá ser encontrada em Stam Ulam, John Von Neumann, and the Monte Carlo method, Los Alamos Science n. 15, pg 131 (1987), artigo livre e disponibilizado pela Los Alamos National Laboratory Research Library. Nesse artigo é apresentado trechos de cartas trocadas entre John von Neuman e Stanislau Ulam. O documento também apresenta uma descrição de 1983 que ajudou a entender a origem dos métodos de Monte Carlo realizada por Stanislaw Ulam, um ano antes do seu falecimento. Abaixo segue uma tradução aproximada do que foi dito:
“Os primeiros pensamentos e tentativas que fiz para praticar [o método de Monte Carlo] foram sugeridos por uma questão que me ocorreu em 1946, quando eu estava convalescendo de uma doença e jogando paciência. A questão é quais são as chances de um jogador sair com sucesso em um jogo de paciência com 52 cartas? Depois de passar muito tempo tentando estimar, por puro cálculo de combinação, eu me perguntei se um método mais prático que o pensamento abstrato não seria expor cem vezes e simplesmente contar o número de jogadas bem-sucedidas. Isso já foi possível prever com o início da nova era de computadores rápidos, e eu imediatamente pensei em problemas de difusão de nêutrons e outras questões de física/matemática, e mais genericamente como mudar processos descritos por certas equações diferenciais em uma forma equivalente interpretável como uma sucessão de operações aleatórias. Mais tarde, … [em 1946, eu] descrevi a ideia à John von Neumann e começamos a planejar cálculos reais.”
— Stanislaw Ulam.
Ulam entendia que as técnicas de amostragem não eram muito utilizadas por envolverem cálculos extremamente demorados, tediósos e sujeito à erros, em uma época em que utilizavam-se dispositivos meânicos para realização de cálculos. Porém, nessa época surgiu o primeiro computador eletrônico, o ENIAC. Embora muito mais lento que os computadores atuais, o ENIAC impressionou Ulam que sugeriu o uso de técnicas de amostragem estatística e da teoria frequentista de probabilidade para simular a difusão de nêutrons em materiais sujeitos à fissão nuclear.
O físico Nicholas Metropolis, que também participou do Projeto Manhattan sugeriu o nome Monte Carlo para o método estatístico. O nome foi inspirado em um tio de Ulam que sempre tomava dinheiro emprestado com parentes para ir jogar no cassino de Monte Carlo, no distrito de Monte Carlo, em Mônaco.
, complexo de jogos e entretenimento localizado no distrito de Monte Carlo, Mônaco.](images/cassino_mc.jpg)
Figura 6.6: Le Casino de Monte-Carlo, complexo de jogos e entretenimento localizado no distrito de Monte Carlo, Mônaco.
Esse fato pode ser lido no artigo The Beginning of the Monte Carlo Method, escrito por Nicholas Metropolis, Los Alamos, 1987, um outro artigo livre e também disponibilizado pela Los Alamos National Laboratory Research Library. Nicholas Metropolis é também responsável pelo desenvolvimento de trabalhos que deram origem ao algoritmo de Mepropolis-Hastings, método de MC muito utilizado na geração de números pseudo-aleatórios de distribuições multidimensionais, especialmente quando o número de dimensões é alto.
6.4.2 Métodos de Monte Carlo
Nos dias atuais, é muito mais fácil codificar uma simulação de MC para obetenção de aproximações que poderiam ser complicadas de serem obtidas analiticamente. Porém, os procedimentos de MC podem ser utilizados para resolver um problema deterministo. Por exemplo, é possível construir um procedimento de MC para aproximar o valor médio de uma função, bem como para calcular uma integral definida de uma função contínua em um intervalo \([a, b]\), sendo estes exemplos notoriamente determinísticos. Porém, os procedimentos de MC são procedimentos que fazem uso de amostragem aleatória massiva para a obtenção de resultados numéricos aproximados. Por exemplo, o método da aceitação e rejeição, apresentado em seções anteriores, é um típico procedimento de MC, uma vez que o método é iterativo e em suas iterações faz uso de geração de observações de uma sequência de variáveis aleatórias. O exemplo que segue mostra a construção de um procedimento simples de MC para o cálculo aproximado do valor médio de uma função.
Exemplo: Calculando o ponto médio de uma função determinística utilizando simulações de MC. Seja \(h(x) = \mathrm{sen}(x)\), tal que \(x \in [0, 2\pi]\). Então, analiticamente, o ponto médio da função \(h(x)\) é dado por:
\[\overline{h} = \frac{1}{2\pi} \int_0^{2\pi} \mathrm{sen}(x) dx = \frac{1}{2\pi}[-\cos(x)] \Big|_0^{2\pi} = -\frac{1}{2\pi}[\cos(2\pi) - \cos(0)] = -\frac{1}{2\pi}\times 0 = 0.\] Lembre-se: O ponto médio de uma função diferenciável no intervalo \([a,b]\) é dado por
\[\overline{h} = \frac{1}{b-a} \int_a^b h(x) dx.\] Para a função em questão, sob um olhar gráfico, temos que:
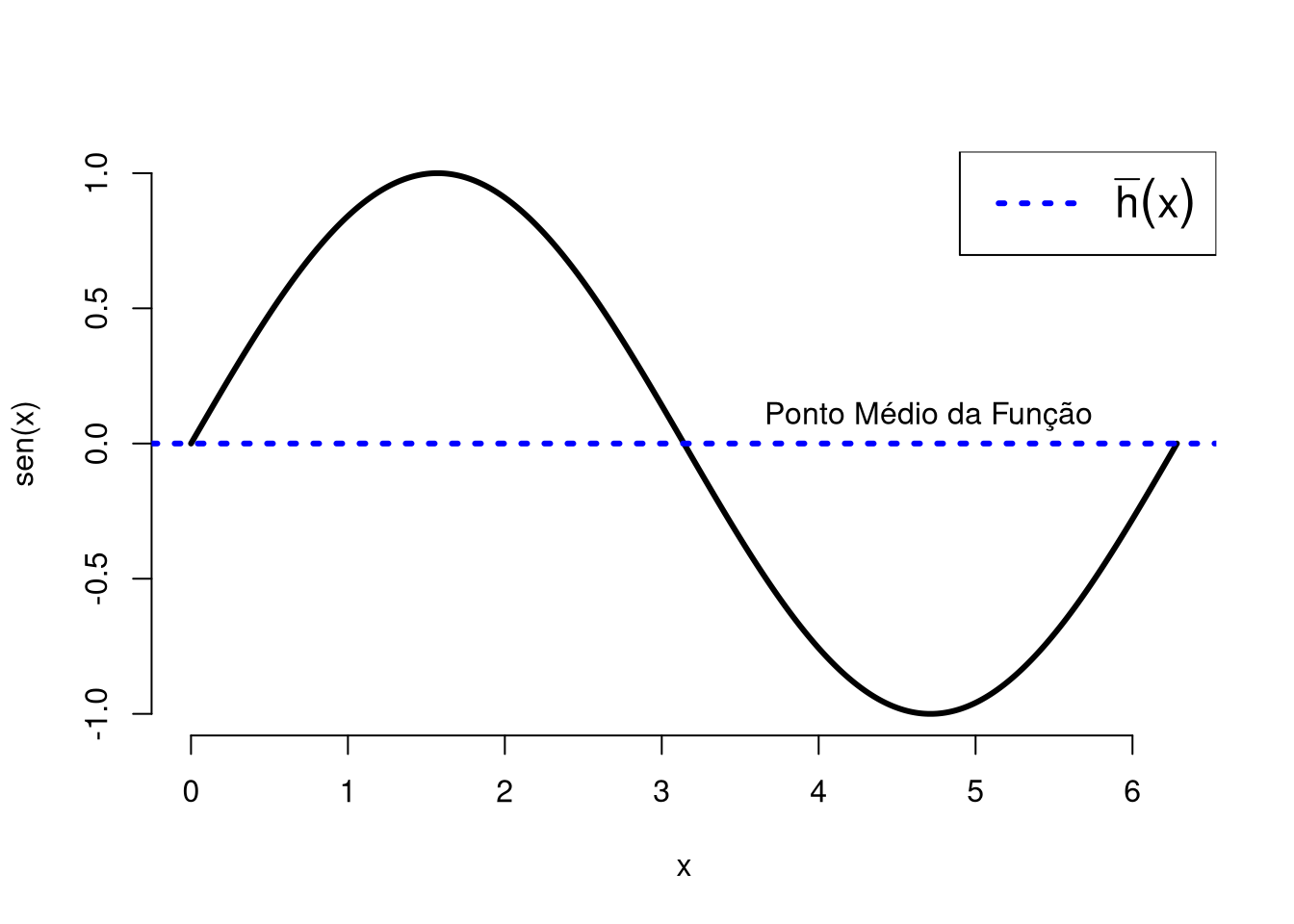
Figura 6.7: Função seno(x), em que a reta azul destaca o ponto médio analítico da função.
Caso não desejássemos calcular a integral acima, o que não justifica-se, uma vez que a integral é bastante simples, poderemos aproximar o valor médio da função \(h(x)\) utilizando uma simples simulação de MC. Para tanto, deveremos selecionar aleatoriamente diversos pontos da função e tirar uma média aritmética. Quanto mais pontos gearmos, melhor será a nossa aproximiação.
# Número de réplicas de Monte Carlo (MC):
N <- 50L
# Fixando uma semente.
set.seed(1L)
# Média dos valores da função:
mean_est <- mean(sin(runif(n = N, min = 0, max = 2 * pi)))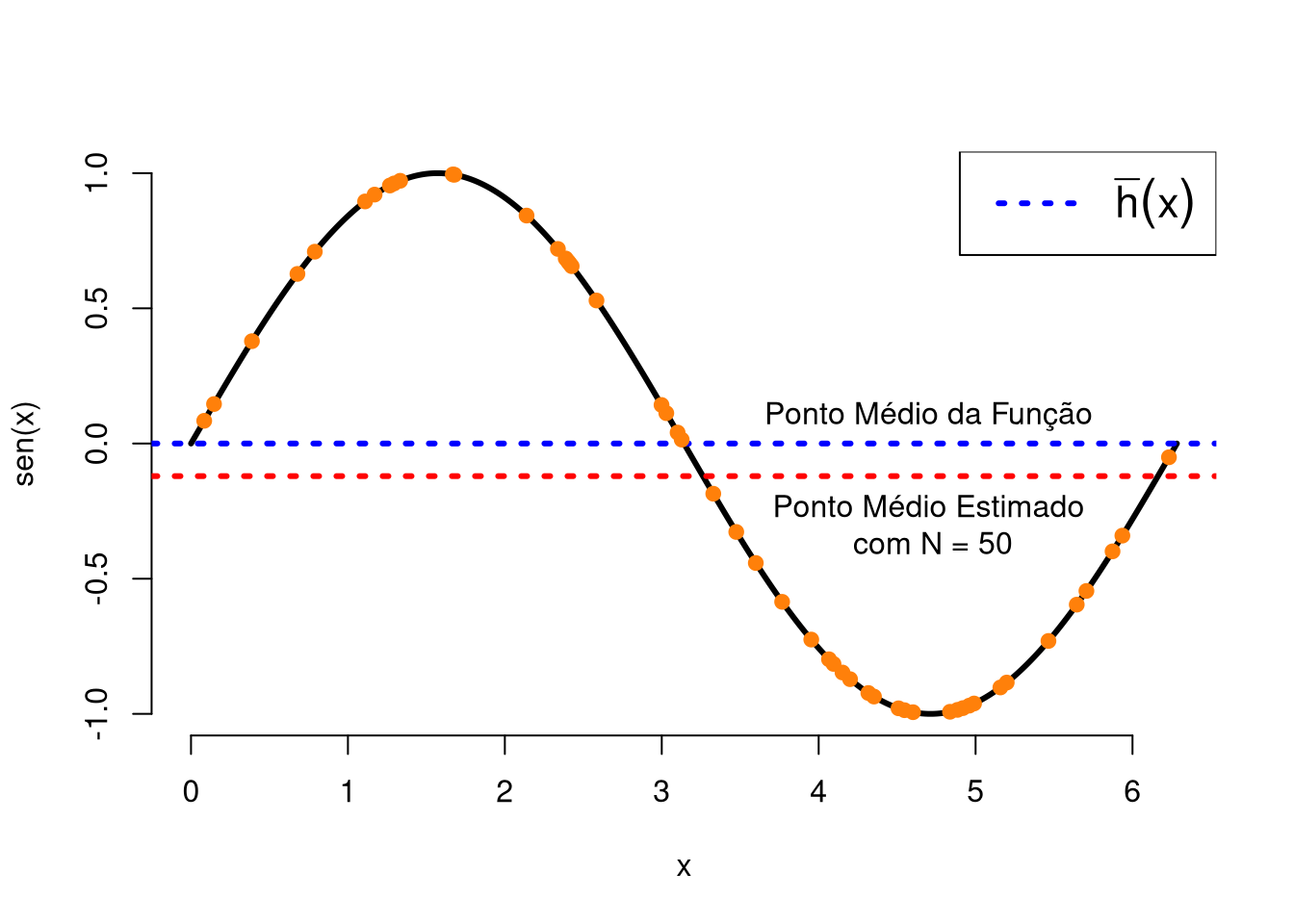
Figura 6.8: Função seno(x), em que a reta azul destaca o ponto médio analítico e a reta em vermelho destaca o ponto médio estimado para 50 réplicas de MC, com os pontos selecionados estão destacados.
6.4.3 Integração por Monte Carlo
O exercício anterior nos fornece tudo que precisaremos para desenvolver um método de MC para o cálculo aproximado de uma integral definida de uma função \(h(x)\) com \(x \in [a, b]\). Se
\[\overline{h} = \frac{1}{b-a}\int_a^b h(x) dx\] e sabemos estimar \(\overline{h}\) pelo método de MC, então saberemos caclular \(\int_a^b h(x) dx\), uma vez que basta fazer:
\[\int_a^b h(x) dx = (b - a)\overline{h},\] em que \(\overline{h}\) é aproximado por MC.
Observação:
Para obtermos uma aproximação para a integral de uma função \(h(x)\) com \(x \in [a, b]\), precisamos apenas calcular o ponto médio da função e multiplicar por \((b-a)\). Dessa forma, estimando o ponto médio de uma função por MC nos conduz diretamente ao método de MC para obter \(\int_a^b h(x) dx\).
Exemplo: Seja \(X\) uma v.a. tal que \(X \sim Weibull(\alpha, \beta)\), com \(\alpha, \beta > 0\) e \(x \geq 0\). Implemente a função intmc(N = 1e3L, fun, lower = NULL, upper = NULL, ...), que aproxima por MC a integral de uma função, em que N é o número de réplicas de MC, fun é a função que desejamos integrar, lower é o limite inferior de integração, upper é o limite superior de integração e ... é o operador dot-dot-dot. Por meio da função intmc() e da função integrate(), obtenha uma aproximação para \(P(X \leq 2)\).
fdp_weibull <- function(x, alpha, beta) dweibull(x, shape = alpha, scale = beta)
intmc <- function(N = 1e3L, fun, lower = NULL, upper = NULL, ...){
if (missing(fun)) stop ("The function has been omitted.")
if (is.null(lower) || is.null(upper)) stop ("Integration limits must be specified.")
# Gerando valores uniformes no suporte da função:
u <- runif(n = N, min = lower, max = upper)
# Valor aproximado da integral:
(upper - lower) * mean(fun(x = u, ...))
}
# P(X < 2):
round(pweibull(q = 2, shape = 1.5, scale = 1.2), digits = 4L)## [1] 0.8837set.seed(1L)
# P(X < 2) por MC:
round(intmc(N = 5e6, fun = fdp_weibull, lower = 0, upper = 2,
alpha = 1.5, beta = 1.2), digits = 4L)## [1] 0.8837O método de integraçao de MC poderá ser entendido também por meio de uma interpretação estatística. Seja \(h(x)\) uma função, com \(x \in [a, b]\) e suponha que desejamos obter uma estimativa para
\[I = \int_a^b h(x) dx.\]
Note que a integral acima poderá ser reescrita, sem alterar o seu resultado, como:
\[I = (b - a) \int_a^b h(x) \frac{1}{b-a}dx.\] Perceba também que se \(X\) é uma v.a., tal que \(X \sim \mathcal{U}(a, b)\), então, \(f_X(x) = \frac{1}{b-a}\), com \(a \leq x \leq b\) é a f.d.p. de \(X\). Dessa forma,
\[\begin{eqnarray} I & = & (b - a) \int_a^b h(x) \frac{1}{b-a}dx = (b - a) \int_a^b h(x) f_X(x)dx = (b - a) \times \mathrm{E}[h(X)]\\ & = & (b - a) \times \mu. \end{eqnarray}\]
Assim, perceba que o problema de calcular \(I\) recai sobre o problema de calcular um valor esperado, isto é, calcular \(\mu\). Dessa forma, precisaremos de um \(\hat{\mu}\) que nos forneça uma boa estimativa para \(\mu\). Consideremos
\[\hat{\mu} = n^{-1}\sum_{i=1}^n h(X_i),\] um estimador para \(\mu\). Dessa forma, temos especificado um estimador para \(I\) que é dado por:
\[\hat{I} = (b - a)\hat{\mu}.\] Perceba que \(\hat{\mu}\) é um estimador não-viesado para \(\mu\). Isso implica que \(\hat{I}\) também será um estimador não-viesado para \(I\). Mais importante, temos que \(\hat{\mu}\) é um estimador consistente para \(\mu\). Isso é verdade, uma vez que se \(X_i, \ldots, X_n\) é uma sequência de v.a.’s i.i.d. em um mesmo espaço de probabilidade, então
\[P\Big(|S_n - n\mu| \geq n\varepsilon\Big) \leq \frac{\mathrm{Var}(S_n)}{\varepsilon^2 n^2},\] pela desigualdade de Chebychev, em que \(S_n = \sum_{i=1}^n h(X_i)\). Como \(X_i, \ldots, X_n\) é uma sequência de v.a.’s i.i.d., tal que \(X_i \sim \mathcal{U}(a,b), \, \forall\, i\), então
\[\mathrm{Var}(S_n) = n \mathrm{Var}[h(X_i)].\] Logo,
\[\lim_{n \to +\infty}P\Big(\Big|S_n - n\mu\Big| \geq n\varepsilon\Big) \leq \lim_{n \to +\infty}\frac{\mathrm{Var}[h(X_i)]}{n\varepsilon^2} = 0,\] uma vez que \(h(x)\) é uma função contínua no intervalo \([a, b]\), logo existe um \(M\) tal que \(|h(X_i)| \leq M, \forall\, i\).
Assim, temos que \(\hat{\mu}\) converge em probabilidade para \(\mu\) (\(\hat{\mu}\) é consistente para se estimar \(\mu\)) e denotamos por \(\hat{\mu} \overset{p}{\to} \mu\). Sendo assim, temos que \(\hat{I}\) é um estimador consistente para \(I\). Isso garante que a medida que tomamos mais pontos, mais nos aproximamos do valor verdadeiro da integral, ou seja, mais nos aproximamos de \(I\).
Note que a variância de \(\hat{I}\) é dada por:
\[\mathrm{Var}(\hat{I}) = (b - a)^2 \mathrm{Var}(\hat{\mu}) = \frac{(b - a)^2}{n}\mathrm{Var}[h(X)].\] Pela definição de variância, temos que
\[\sigma^2 = \mathrm{Var}(\hat{I}) = \mathrm{E}\Big(\hat{I}^2\Big) - E^2(\hat{I}) = \gamma - \eta^2.\] Assim, um estimador para \(\mathrm{Var}(\hat{I})\) também poderá ser obtido utilizando um procedimento de MC, de tal forma que:
\[\widehat{\sigma}^2 = \widehat{\mathrm{Var}(\hat{I})} = \overline{\widehat{\gamma}} - \overline{\widehat{\eta}}^2,\]
em que \(\overline{\widehat{\gamma}} = n^{-1} \sum_{i=1}^n \hat{I}_i^2\) e \(\overline{\widehat{\eta}}^2 = \Big(n^{-1}\sum_{i=1}^n\hat{I}_i\Big)^2\). Perceba que \(\hat{I}_i\) é obtido por um procedimento de MC para cada \(i\), com \(i = 1, \ldots, n\). Sendo assim, necessitamos de várias estimativas da integral para se obter uma estimativa de \(\mathrm{Var}(\hat{I})\) que também é um procedimento de MC.
Exemplo: Abaixo é implementado a função intvarmc(N = 1e3L, fun, lower = NULL, upper = NULL, ...) que retona uma estimativa para a integral de uma função, a variância estimada por MC do estimador \(\hat{I}\) e um vetor de estimativas \(\hat{I}\) utilizados para o cálculo de \(\widehat{\mathrm{Var}(\hat{I})}\) por MC. Em que
Né a quantidade de réplicas de MC. Por padrãoN = 1e3L;funé a função contínua que desejamos integrar;loweré o limite inferior de integração;upperé o limite superior de integração;...é o argumento dot-dot-dot (varargs) que será útil para passarmos outros argumentos à função que desejamos integrar.
fdp_weibull <- function(x, alpha, beta) dweibull(x, shape = alpha,
scale = beta)
intmc <- function(N = 1e3L, fun, lower = NULL, upper = NULL, ...){
if (missing(fun)) stop ("The function has been omitted.")
if (is.null(lower) || is.null(upper)) stop ("Integration limits must be specified.")
# Gerando valores uniformes no suporte da função:
u <- runif(n = N, min = lower, max = upper)
# Valor aproximado da integral:
(upper - lower) * mean(fun(x = u, ...))
}
# Essa função retorna uma estimativa da integral de uma função h(x) por MC
# uma estimativa da da variância do estimador de MC para integral de h(x):
intvarmc <- function(N = 1e3L, fun, lower = NULL, upper = NULL, ...){
intmc_map <- function(x, ...) intmc(N, fun, lower, upper, ...)
i_hat <- purrr::map_dbl(.x = 1:N, .f = intmc_map, ...)
var_hat <- mean(i_hat ^ 2) - mean(i_hat) ^ 2
list(i_hat = mean(i_hat), var_hat = var_hat, vec_ihat = i_hat)
}
set.seed(0L)
result <- intvarmc(N = 5e3L, fun = fdp_weibull, lower = 0, upper = 10,
alpha = 1.5, beta = 1.5)
str(result)## List of 3
## $ i_hat : num 1
## $ var_hat : num 0.000503
## $ vec_ihat: num [1:5000] 1.029 0.975 0.999 1.005 1.031 ...# Realizando um teste de normalidade pelo
# teste de Shapiro-Wilk:
shapiro.test(result$vec_ihat)##
## Shapiro-Wilk normality test
##
## data: result$vec_ihat
## W = 0.99969, p-value = 0.6642Uma vez que são médias, perceba que as estimativas obtidas por \(\hat{I}_1, \ldots, \hat{I}_n\) aparentemente segue uma distribuição normal, em que \(\hat{I}_i \sim \mathcal{N}(I, \sigma^2/n)\), o que é garantido pelo Teorema Central do Limite.
Construindo um histograma e realizando um teste de normalidade, temos:
hist(result$vec_ihat, main = expression(paste("Estimativas ", hat(I)[i])),
xlab = expression(hat(I)[i]), ylab = "Frequência",
border = NA, col = rgb(1, 0.9, 0.8))
Observação:
Note que a distribuição de \(\hat{I}_i, \forall \, i\) é centrada no valor da integral que desejamos calcular. No caso do exercício acima, como a função é uma f.d.p, então a distribuição será centrada em 1.
6.4.4 Aproximando o valor de \(\pi\)
Uma outra aplicação bastante conhecida dos métodos de MC é a obtenção de um valor aproximado para a constante \(\pi\). O método para aproximação do valor de \(\pi\) é construído considerando inicialmente uma circunferência de raio (\(r = 1\)) na seguinte forma:
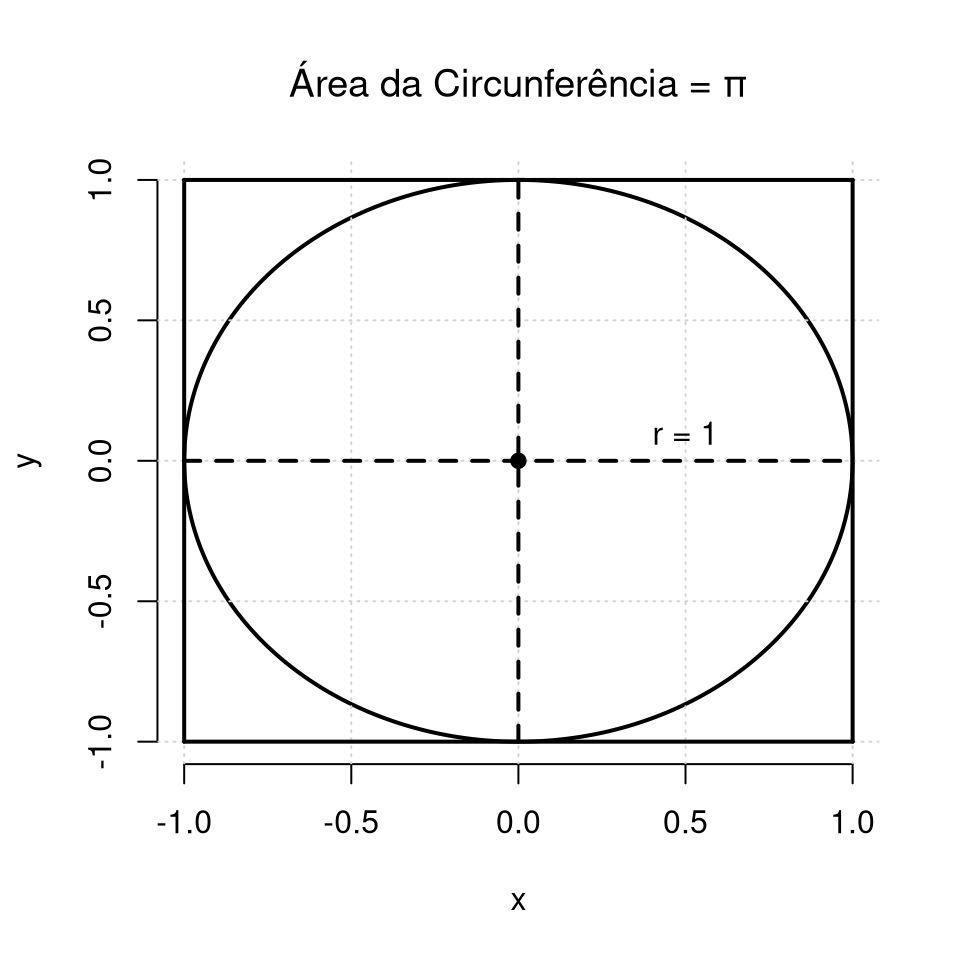
Figura 4.4: Cicunferência centrada no ponton (0,0) de raio igual à 1 (um) e de área igual à constante de desejamos estimar.
A estatégia por meio de um procedimento de MC é gerar massivamente (mil, 10 mil, 100 mil, …) pontos no interior do quadrado de área 1. Dessa forma, deveremos contabilizar a quantidade de pontos que cairam no interior da circunferência e dividir pelo total de pontos, isto é, desejamos obter a proporção de pontos que cairam dentro da circunferência, onde teremos, assim, uma aproximação da área. Porém, perceba que poderemos nos restringir ao primeiro quadrante, com área igual à \(\frac{\pi}{4}\). Dessa forma, considerando apenas o primerio quadrante, temos que a porporção de pontos que caem no interior da circunferência multiplicada por 4 irá fornecer uma aproximação para o valor de \(\pi\).
Exemplo: Implemente a função insideplot(x, y) que recebe como argumentos dois vetores de mesmo comprimento. A função deverá construir um gráfico do primeiro quadrante da circunferência, em um quadrado unitário, com os pontos formados pelos valores dos vetores, par a par, destancando de vermelho os pontos no interior da circunferência e de azul àqueles que caem fora dela.
insideplot <- function(x, y) {
plot.new()
plot.window(xlim = c(0, 1), ylim = c(0, 1))
axis(1); axis(2)
title(xlab = "x", ylab = "y")
x_circ <- seq(0, 1, length.out = 1000L)
y_circ <- sqrt(1 - x_circ ^ 2)
test <- function(x, y){
if ((x ^ 2 + y ^ 2) <= 1) points(x, y, col = "red", pch = 19)
else points(x, y, col = "blue", pch = 19)
}
segments(0, 0, 1, 0, lwd = 2); segments(0, 0, 0, 1, lwd = 2)
segments(0, 1, 1, 1, lwd = 2); segments(1, 0, 1, 1, lwd = 2)
lines(x_circ, y_circ, lwd = 2L)
invisible(mapply(FUN = test, x, y))
}
x <- c(0.42, 0.24, 0.81, 0.93)
y <- c(0.21, 0.47, 0.72, 0.85)
insideplot(x, y)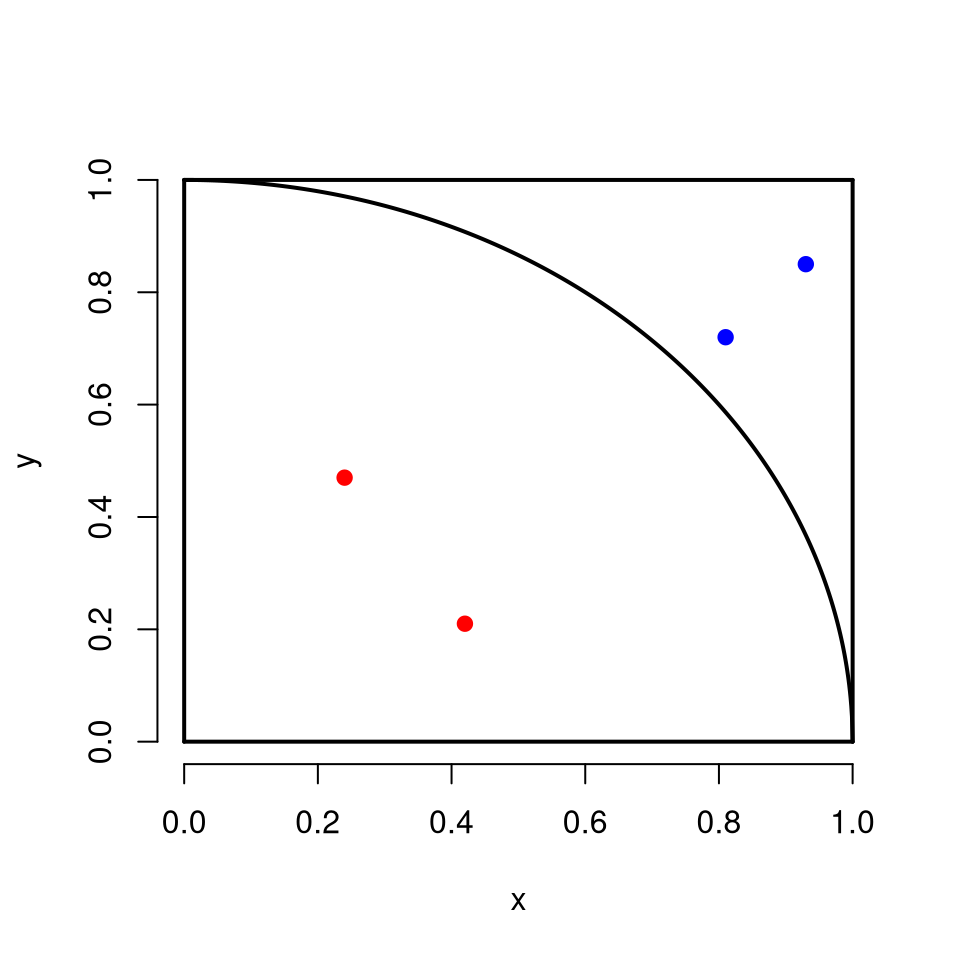
Figura 6.9: Resultado do uso da função insideplot() nos pontos (0.42, 0.21), (0.24, 0.47), (0.81, 0.72) e (0.93, 0.85), em que pontos vemelhos estão no interior da circunferência e pontos azuis fora dela.
Exemplo: Implementando a função mcpi(N = 1e3L) que aproxima o valor da constante \(\pi\) por meio de um procedimento de MC. A função mcpi() retornará o valor aproximado da constante \(\pi\) e construirá o gráfico com os pontos gerados utilizando a função insideplot().
# Aproximando o valor da constante pi por MC:
mcpi <- function(N = 1e3L){
x <- runif(n = N, min = 0, max = 1)
y <- runif(n = N, min = 0, max = 1)
inside <- function(x, y) ifelse((x ^ 2 + y ^ 2) <= 1, TRUE, FALSE)
insideplot(x, y)
4 * sum(mapply(FUN = inside, x, y)) / N
# ou sum(purrr::map2_lgl(.x = x, .y = y, .f = inside)) / N
}
# Fixando uma semente:
set.seed(1L)
# Aproximando o valor de pi (mil réplicas):
mcpi()
## [1] 3.1486.4.5 Paralelizando um procedimento de Monte Carlo
A classe de procedimentos de MC contemplam metodologias típias que podem ser paralelizadas, isto é, por se tratarem de procedimentos iterativos, cada iteração poderá ser realizada em paralelo. Porém, é importante deixar claro que nem todo o procedimento iterativo poderá ser paralelizado. Essa é uma restrição do ponto de vista matemático e não do ponto de vista de computação. Isso deve-se ao fato de que nem todos procedimentos iterativos são matematicamente independentes, isto é, nesses procedimentos, para realizarmos a iteração \(t + 1\) necessariamente devemos esperar pelos cálculos realizados na \(t\)-ésima iteração.
Tipicamente, os procedimentos de MC são matematicamente independentes. Embora a construção de tais procedimentos que produzem amostras com as propriedades desejadas geralmente não seja difícil, a tarefa de garantir a convergência a uma taxa compatível com os recursos computacionais atuais continua sendo um grande desafio.
Nos dias atuais, é comum observarmos códigos passíveis de paralização sem fazer o devido aproveitamento de todos os recursos computacionais disponíveis em um dado computador. Em dias atuais, é comum processadores e GPUS (Graphics Processing Unit) com vários núcleos de processamento.
A linguagem R disponibiliza diversas bibliotecas para se trabalhar com computação paralela. Ente alguns pacotes importantes que viablizam o uso de computação paralela em R destaco o parallel e o snow (“Simple Network of Workstations”). Tempos atrás, havia também o pacote multicore que foi removido do CRAN, sendo substituído pelo pacote parallel.
Diversas funções do pacote parallel são derivadas do pacote snow e do antigo pacote multicore. O pacote parallel reúne as melhores características desses pacotes, com algumas modificações e características próprias. Além desses pacote, há diversas outas bibliotecas em R disponíveis para implementação de códigos paralelizados. Porém, a maioria dessas bibliotecas utilizam-se do parallel e snow como backend para suas implementações. Por exemplo, foreach + doParallel normalmente são utilizados em conjunto para a criação de loops com execução em paralelo, em que utiliza-se das funções foreach() + %dopar% do pacote foreach. Nesse exemplo, o pacote doParallel atuará como uma interface para o pacote parallel que é o verdadeiro responsável para efetuar a paralelização do loop.
Uma das vantagem do pacote parallel está no fato dele ser distribuído em conjunto com a linguagem R. Mais precisamente, o pacote parallel foi incluído, pela primeira vez, em 31 de Outubro de 2011, na versão 2.14.0 da linguagem R. Uma outra vantagem do pacote parallel é que ele necessita de menos configurações iniciais para a utilização dos seus funcionais em um procedimento de paralização multicore em um mesmo processador.
A única desvantagem do pacote parallel diz respeito aos usuários do sistema operacional (SO) Windows, em que alguns de seus funcionais não irão funcionar de forma paralela. Porém, o pacote parallel dispõe de funcionais alternativos para a realização de computação paralela em Windows. A vantagem de utilizar-se um sistema *nix é que os funcionais que funcionam em Windows também funcionarão em sistemas *nix.
Aqui trataremos apenas da paralelização multicore de memória compartilhada em um único processador, isto é, em um mesmo chip, utilizando a linguagem R. Para os exemplos, utilizaremos os típicos procedimentos de MC que são passíveis de execução em paralelo.
Processadores com múltiplos núcleos são muito comuns nos dias atuais. Também é comum estamos implementando nossas simulações em computadores pessoais que normalmente possue apenas um único processador com vários núcleos de processamento. A ideia é discutir como aproveitarmos todo o recurso computacional desses processadores e assim usufruirmos de um código com maior performance, uma vez que temos esses recursos a nossa disposição. Abaixo encontra-se uma representação típica de um processador com vários núcleos de processamento, mais precisamente, 4 (cores) destacados em azul e 8 (oito) threads destacados em vermelho.
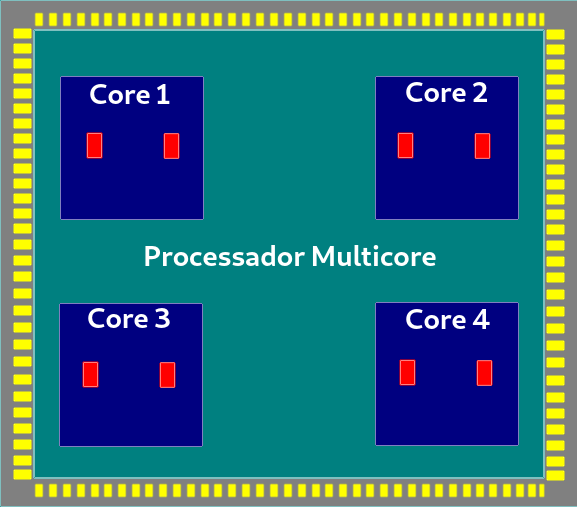
Figura 6.10: Representação de um processador multicore (múltiplos núcleos), em que os retângulos vermelhos representam os pseudo-cores (hardware threads) e a parte cinza onde encontra-se o processador chamamos de soquete.
Abaixo encontram-se listados alguns conceitos comumente utilizados em computação paralela. Entender essas nomenclaturas ajudará bastante a compreensão de textos em computação paralela.
Nó: um único computador que consiste basicamente de uma placa-mãe com uma memória e um processador;
Processador/soquete: a unidade física que contém um ou mais núcleos que fazem cálculos;
Core/núcleo: a menor unidade de computação do processador. Cada core é capaz de executar um único programa/tarefa;
Thread (hardware): também conhecido como core lógico, as threads, do ponto de vista de hardware, são unidades de computação dentro dos cores que poderá permitir que um core faça duas ou mais tarefas ao mesmo tempo.
Trabalhador/worker: um processo independente que conduz o cálculo e fornece os resultados para o processo mestre/master. Alguns texto referem-se aos trabalhadores como threads (software), em que thread mestre/thread master é o processo mestre e as bifurcações geridas por esse processo principal em outros processos são chamados de threads escravas/slave threads.
Importante:
Com o pacote parallel é possível também fazer uso de computação paralela utilizando Message Passing Interface - MPI (um padrão de dados em computação paralela), quando temos a nossa disposição um cluster configurado com várias máquina (vários nós), cada um com vários processadores com múltiplos núcleos de processamento.
Também é importante deixar destacar que nem sempre os custos que o computador tem em gerir diversos processos justifica a paralelização de um código. Por exemplo, é possível que um código funcione de forma mais eficiente quando executado de forma serial quando comparado ao seu análogo paralelo.
6.4.6 Speedup
Uma forma de mensurar o ganho ou perda computacional ao executar um código em paralelo é utilizando a medida speedup que é definido como a relação de tempo gasto para executar uma terefa de forma serial com o tempo gasta para executar a mesma tarefa em \(n\) threads. Ou seja, se \(S\) é o speedup, então
\[S(n) = \frac{T(1)}{T(n)},\] em que \(T(1)\) é o tempo serial e \(T(n)\) é o tempo em paralelo ao considerar \(N\) cores, em um processador que suporta essa quantidade de núcleos. Assim, quanto maior o speedup, maior será o ganho computacional ao se paralelizar um código.
Lei de Amdahl
Se o tempo de processamento de uma tarefa pode ser escalonado linearmente com o número de núcleos utilizados em paralelo, dizemos que o código em paralelo produz uma aceleração linear, sendo este o melhor dos cenários. Porém, na maioria dos problemas em que desejamos paralelizar, o tempo de computação atinge uma “parede assintótica,” em que os benefícios de utilizar núcleos adicionais são compensados pelos custos adicionais de gerenciar o fluxo de informações entre tantos trabalhadores. Essa função assintótica poderá seguir a Lei de Amdahl, definida por Gene Myron Amdahl, em uma conferência, em 1967. A lei diz que:
\[T(n) = T(1)\Big[s + \frac{1}{n}(1 - s)\Big],\] em que \(T(n)\) é o tempo que um algoritmo leva para ser executado de forma paralela utilizando \(n\) núcleos e \(s\) é a proporção do código que deve ser executado de forma serial, sendo \(1 - s\) a proporção de código executado de forma paralela.
Sendo assim, dado \(s\), o speedup teórico é dado por:
\[S(n) = \frac{T(1)}{T(n)} = \frac{T(1)}{T(1)\Big[s + \frac{1}{n}(1 - s)\Big]} = \frac{1}{s + \frac{1}{n}(1-s)}.\] Perceba que,
\[\lim_{n \to \infty} \frac{1}{s + \frac{1}{n}(1-s)} = \frac{1}{s},\] é o speedup máximo alcançado, segundo essa lei.
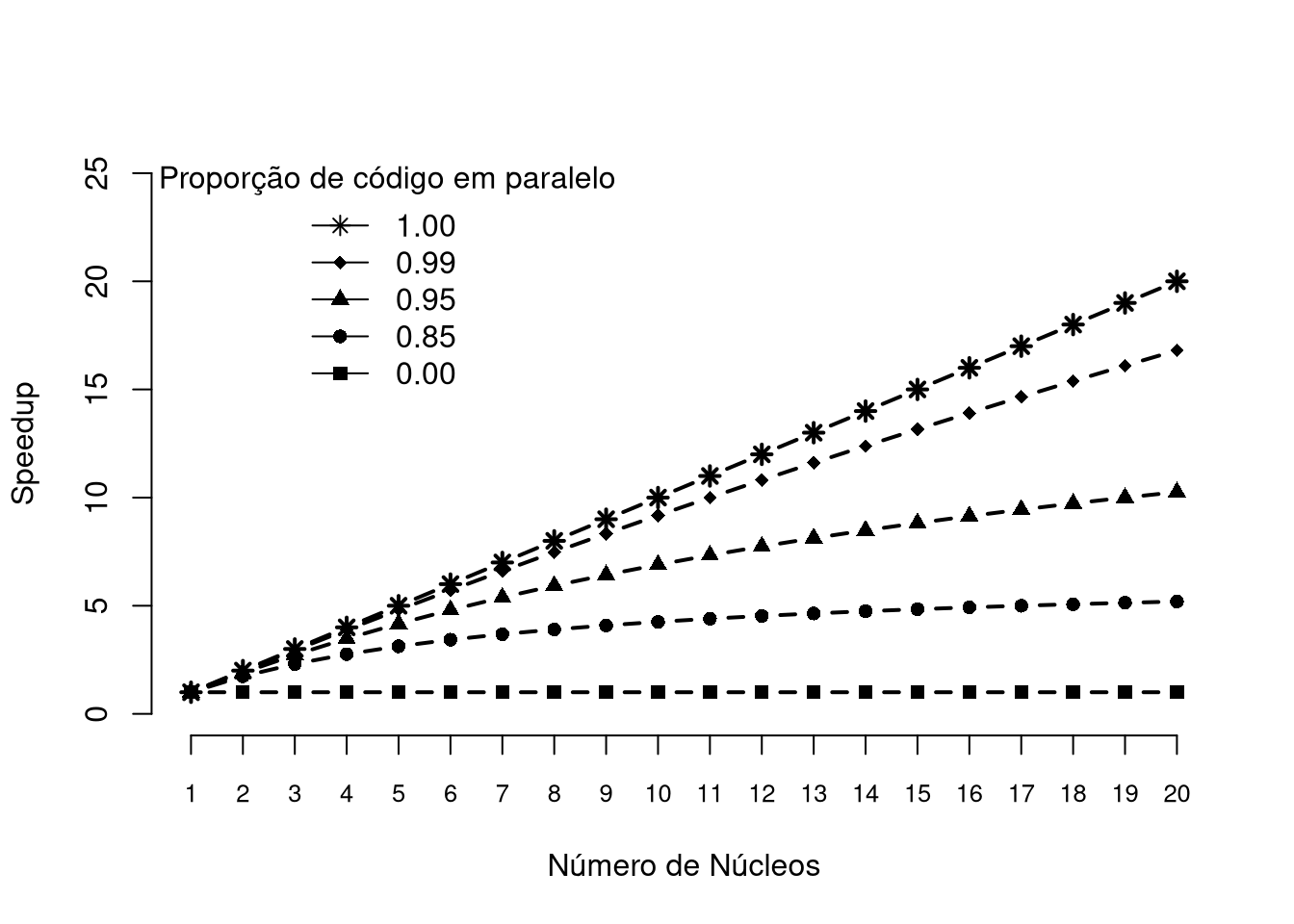
Figura 6.11: Speedup estimado utilizando a Lei de Amdhal levando em consideração a quantidade de núcleos disponiveis e a proporção de código passível de paralelização de um algoritmo.
Nota:
Existem diversas métricas para entender o comportamento de um aplicação paralela em face ao número de núcleos utilizados, em que todas elas tem suas limitações. A principal limitação da Lei de Amdahl é o fato dela ingnorar ao gerenciar-se diversos processos.
O que é mais importante para os nossos objetivos é a consciência da existência de uma barreira assintótica para o speedup. Na prática, essa barreira torna-se-á bastante frequênte devido aos custos computacionais relacionados ao transporte de dados entre os processos que será muito provavelmente diminuído com o passar dos anos.
6.4.7 Pacote parallel
O pacote parallel possui diversas funções úteis. Você poderá encontrar um tutorial do parallel clicando aqui. O pacote parallel possui diversas funções úteis, em que um vetor completo com o nome das funções pode ser obtido fazendo:
library(parallel)
ls("package:parallel")## [1] "clusterApply" "clusterApplyLB" "clusterCall"
## [4] "clusterEvalQ" "clusterExport" "clusterMap"
## [7] "clusterSetRNGStream" "clusterSplit" "detectCores"
## [10] "getDefaultCluster" "makeCluster" "makeForkCluster"
## [13] "makePSOCKcluster" "mc.reset.stream" "mcaffinity"
## [16] "mccollect" "mclapply" "mcMap"
## [19] "mcmapply" "mcparallel" "nextRNGStream"
## [22] "nextRNGSubStream" "parApply" "parCapply"
## [25] "parLapply" "parLapplyLB" "parRapply"
## [28] "parSapply" "parSapplyLB" "pvec"
## [31] "setDefaultCluster" "splitIndices" "stopCluster"As funções que serão destacadas aqui e que nos ajudaram a paralelizar um procedimento de MC são as funções mclapply(), mcmapply(), mcMap() e detectCores(). Perceba que algumas funções iniciam-se com mc, o que faz alusão à expressão multicore (múltiplos núcleos). Dessa forma, mclapply() equivale ao funcional lapply(), porém trabalhando de forma paralela, mcmapply() é análogo paralelo do funcional mapply() e mcMap() é o analogo paralelo do funcional Map().
As funções mclapply() e mcmapply() trabalham de forma multicore, ou seja, sobre um único processador com vários núcleos físicos e lógicos. Isso é feito utilizando o conceito de FORK, sendo este um conceito de sistemas operacionais POSIX que está disponível em todas as plataformas R, exceto em Windows. O sistema FORK cria um novo processo de R tomando uma cópia completa do processo mestre, incluindo o espaço de trabalho e o estado de fluxo de números aleatórios. Porém, em um SO razoável, as cópias compartilham páginas de memória com o processo mestre até o momento em que o que é comum entre entre os processos seja modificado, permitindo assim que este procedimento de FORK seja eficiente.
Exemplo: Comparando a execução serial e paralela da função intvarmc(). Como é possível observar, optou-se em paralelizar a função intmc() que é utilizado pela função intvarmc() para o cálculo das integrais aproximadas por um procedimento de MC. É possível observar que paralelizar a execução da função intvarmc() contribuiu significativamente na melhoria da peformance da função intvarmc(). Observe as saídas dos tempos de execução das funções intvarmc() (função com execução serial) e intvarmc_parallel() (cópia paralelizada da função intvarmc()):
Código Serial:
# Código Serial -----------------------------------------------------------
intvarmc <- function(N = 1e3L, fun, lower = NULL, upper = NULL, ...){
intmc_map <- function(x, ...) intmc(N, fun, lower, upper, ...)
i_hat <- purrr::map_dbl(.x = 1:N, .f = intmc_map, ...)
var_hat <- mean(i_hat ^ 2) - mean(i_hat) ^ 2
list(i_hat = mean(i_hat), var_hat = var_hat, vec_ihat = i_hat)
}
set.seed(0L)
time_serial <- system.time(result_serial <-
intvarmc(N = 5e3L, fun = fdp_weibull,
lower = 0, upper = 10,
alpha = 1.5, beta = 1.5))
result_serial$i_hat## [1] 1.000779Código Paralelizado:
# Código Paralelizado -----------------------------------------------------
intvarmc_parallel <- function(N = 1e3L, fun, lower = NULL, upper = NULL, ...){
intmc_map <- function(x, ...) intmc(N, fun, lower, upper, ...)
# Reescrita da função intmc() para que seja possível utilizar
# em um funcional baseado no funcional lapply().
i_hat <- unlist(parallel::mclapply(X = 1L:N, FUN = intmc_map, ...,
mc.cores = parallel::detectCores()))
var_hat <- mean(i_hat ^ 2) - mean(i_hat) ^ 2
list(i_hat = mean(i_hat), var_hat = var_hat, vec_ihat = i_hat)
}
set.seed(0L)
system.time(result_parallel <- intvarmc_parallel(N = 5e3L, fun = fdp_weibull,
lower = 0, upper = 10,
alpha = 1.5, beta = 1.5))## usuário sistema decorrido
## 5.204 1.389 1.535result_parallel$i_hat## [1] 1.000073Importante:
O código paralelizado no exemplo anterior irá verdadeiramente funcionar de forma paralela em sistemas *nix e não trabalhará corretamente em Windows. Isso se deve ao fato de muitas funções do pacote parallel serem derivadas do pacote multicore e utilizarem FORK, uma chamada de sistema POSIX não compatível com o SO Windows. Essas funções, em que FORK é apenas uma delas, constroem uma interface entre um processo e o SO.
Em Windows, uma abordagem paralelizada também poderá ser implementada utilizando o pacote parallel, a custo de um pouco mais de passos, já que não há suporte à FORK. Como função mclapply() e funções derivadas fazem uso de FORK, deveremos considerar funções que não fazem uso de FORK.
Exemplo: Implementação da função intvarmc_parallel() para que funcione de forma paralelizada em Windows. Perceba que foi necessário incluir mais passos e substituir a função mclapply() pela função parLapply() que também está disponível no pacote parallel.
Assim como o FORK, o PSOCK é também uma chamada de sistema POSIX que define uma nova forma de transporte de dados e comunicação entre as threads e o processo mestre. O PSOCK faz algumas execuções do comando Rscript, conforme a quantidade de núcleos utilizados para realizar um trabalho. Nesse sistema, a comunicação das threads com o processo mestre se dá utilizando conecções de soquete. Sendo assim, quando deseja-se fazer uso de paralelismo multicore, em Windows, há a necessidade da criação de um cluster do tipo PSOCK.
Nota:
É sempre uma boa prática desligar as theads chamando a função stopCluster() ao final da execução da função em paralelo, muito embora em alguns tipos de clusters o encerramento é automático. Caso contrário, poderemos correr o risco de transbordar threads, por exemplo, se o tipo de cluster for alterado, o que poderá gerar diversos conflitos e inconsistências.
# No Windows --------------------------------------------------------------
# Atribuindo a quantidade de núcleos disponíveis.
cores <- getOption("mc.cores", parallel::detectCores())
# Criando um cluster do tipo PSOCK.
cl <- makeCluster(cores, type = "PSOCK")
# Exportando as funções intmc() e fdp_weibull() para que sejam reconhecidas
# em cada núcleo.
clusterExport(cl = cl, varlist = c("intmc", "fdp_weibull"), envir = environment())
intvarmc_parallel <- function(N = 1e3L, fun, lower = NULL, upper = NULL, ...){
# Reescrita da função intmc() para que seja possível utilizar
# em um funcional baseado no funcional lapply().
intmc_map <- function(x, ...) intmc(N, fun, lower, upper, ...)
i_hat <- unlist(parallel::parLapply(cl = cl, X = 1L:N, fun = intmc_map, ...))
var_hat <- mean(i_hat ^ 2) - mean(i_hat) ^ 2
list(i_hat = mean(i_hat), var_hat = var_hat, vec_ihat = i_hat)
}
set.seed(0L)
system.time(result_parallel <- intvarmc_parallel(N = 5e3L, fun = fdp_weibull,
lower = 0, upper = 10,
alpha = 1.5, beta = 1.5))
stopCluster(cl)
result_parallel$i_hatTanto no exemplo de paralização em SO *nix utilizando FORK quanto em Windows utilizando um cluster PSOCK, a função intvarmc_parallel() mostrou-se mais eficiente do sua implementação serial. Porém, nos deparamos com o problema de reprodutibilidade. Perceba que fazer set.seed(0L) antes da execução da função intvarmc_parallel() não é suficiente para garantir os mesmos resultados. Como é de responsabilidade do SO distribuir os processos entre as threads (hardware) disponíveis e o gerador de números pseudo-aleatórios toma estados distintos a depender da thread (hardware) ao qual um trabalhador foi alocado, sequências distintas muito provavelmente serão observadas entre execuções de uma função paralelizada.
O pacote parallel contém uma implementação das ideias de L’Ecuyer et al. (2002), cujo o artigo é livre e poderá ser acessado com o link abaixo:
L’Ecuyer P, Simard R, Chen EJ, Kelton WD (2002). An object-oriented random-number package with many long streams and substreams. Operations Research, 50, 1073–5. URL link.
Assim, em R, é possível fazer uso desse gerador que recebe o nome L’Ecuyer-CMRG. Isso poderá ser feito passando a string "L'Ecuyer-CMRG", alem da semente, para o agumento kind da função set.seed() ou alterando o gerador utilizando a função "RNGkind()" e posteriormente utilizando a função set.seed() para fixar uma semente. As duas formas estão apresentadas abaixo:
# Forma 1:
set.seed(seed = 0L, kind = "L'Ecuyer-CMRG")
# Forma 2:
RNGkind(kind = "L'Ecuyer-CMRG")
set.seed(0L)Exemplo: Reproduções da função intvarmc_parallel() usando os sistemas FORK e PSOCK, repectivamente. Trata-se de um exemplo que poderá ser reproduzível, uma vez que foi utilizado o gerador L’Ecuyer-CMRG com semente fixa.
Paralelização usando FORK:
# Código Paralelizado -----------------------------------------------------
intvarmc_parallel <- function(N = 1e3L, fun, lower = NULL, upper = NULL, ...){
intmc_map <- function(x, ...) intmc(N, fun, lower, upper, ...)
# Reescrita da função intmc() para que seja possível utilizar
# em um funcional baseado no funcional lapply().
i_hat <- unlist(parallel::mclapply(X = 1L:N, FUN = intmc_map, ...,
mc.cores = parallel::detectCores()))
var_hat <- mean(i_hat ^ 2) - mean(i_hat) ^ 2
list(i_hat = mean(i_hat), var_hat = var_hat, vec_ihat = i_hat)
}
# Fixando uma semente para um gerador que poderá
# trabalhar sobre processos paralelizados.
set.seed(0L, kin = "L'Ecuyer-CMRG")
time_parallel <- system.time(result_parallel <-
intvarmc_parallel(N = 5e3L, fun = fdp_weibull,
lower = 0, upper = 10,
alpha = 1.5, beta = 1.5))
# Uma aproximação para integral de uma função
# utilizando um procedimento de MC:
result_parallel$i_hat## [1] 0.9993872# Tempo em serial:
time_serial[3]## elapsed
## 4.353# Tempo em paralelo:
time_parallel[3]## elapsed
## 1.349# Speedup:
time_serial[3]/time_parallel[3]## elapsed
## 3.226835Paralelização usando PSOCK:
# No Windows --------------------------------------------------------------
# Atribuindo a quantidade de núcleos disponíveis.
cores <- getOption("mc.cores", parallel::detectCores())
# Criando um cluster do tipo PSOCK.
cl <- makeCluster(cores, type = "PSOCK")
# Exportando as funções intmc() e fdp_weibull() para que sejam reconhecidas
# em cada núcleo.
clusterExport(cl = cl, varlist = c("intmc", "fdp_weibull"), envir = environment())
intvarmc_parallel <- function(N = 1e3L, fun, lower = NULL, upper = NULL, ...){
# Reescrita da função intmc() para que seja possível utilizar
# em um funcional baseado no funcional lapply().
intmc_map <- function(x, ...) intmc(N, fun, lower, upper, ...)
i_hat <- unlist(parallel::parLapply(cl = cl, X = 1L:N, fun = intmc_map, ...))
var_hat <- mean(i_hat ^ 2) - mean(i_hat) ^ 2
list(i_hat = mean(i_hat), var_hat = var_hat, vec_ihat = i_hat)
}
# Fixando uma semente para um gerador que poderá
# trabalhar sobre processos paralelizados.
set.seed(0L, kin = "L'Ecuyer-CMRG")
system.time(result_parallel <- intvarmc_parallel(N = 5e3L, fun = fdp_weibull,
lower = 0, upper = 10,
alpha = 1.5, beta = 1.5))
stopCluster(cl)
# Uma aproximação para integral de uma função
# utilizando um procedimento de MC:
result_parallel$i_hat
# Speedup:
time_serial[3]/time_parallel[3]Exercício
1 - Explique o que é um procedimento de Monte Carlo (MC)?
2 - Enuncie um procedimento de MC para o cálculo de uma integral de uma função contínua em um intervalo \([a, b]\). Depois, escreva um algoritmo para o procedimento enunciado.
3 - Seja \(\hat{I}\) o estimador de \(I = \int_a^b f(x) dx\), em que \(f\) é uma função contínua no intervalo \([a, b]\), em que
\[\hat{I} = (b-a) \frac{\sum_{i=1}^n f(x_i)}{n},\] cuja amostra é obtida pelo procedimento de MC enunciado no exercício anterior. Mostre que \(\hat{I}\) é um estimador não-viesado e consistente para \(I\).
4 - Implemente a função intmc() que calcula a integral de uma função contínua qualquer definida em um intervalo \([a, b]\). Dica: Utilize o operador dot-dot-dot (operador varargs) para que a função intmc() possa receber argumentos da função que será integrada por um procedimento de MC.
5 - Seja \(X_1, \ldots, X_n\) uma amostra aleatória de v.a.’s tal que \(X_i \sim \mathcal{N}(\mu = 0, \sigma^2 = 1)\). Construa um procedimento de MC para avaliar os estimadores \(\hat{\sigma}^2\) e \(S^2\) de \(\sigma^2\), em que
\[\begin{eqnarray} \hat{\sigma}^2 &=& \frac{1}{n}\sum_{i=1}^n (X_i - \overline{X})^2\\ &\mathrm{e}&\\ S^2 &=& \frac{1}{n - 1}\sum_{i=1}^n (X_i - \overline{X})^2. \end{eqnarray}\]
Dica: Para comparar, utilize uma aproximação do Erro Quadrático Medio (EQM) obtida por um procedimento de MC. Lembre-se, se \(\hat{\theta}\) é um estimador para \(\theta\), então o \(\mathrm{EQM}(\hat{\theta}) = \mathrm{E}[(\hat{\theta} - \theta)^2]\).
6 - Um dado experimento aleatório consiste em lançar dois dados não viesados (6 lados em cada dado) e observar a soma obtida. Por meio de um procedimento de MC, obtenha a probabilidade aproximada da soma ser par. Simule para \(N = 10, 100, 1000, 10000\) e \(100000\), em que \(N\) é o número de réplicas de MC. O que você observa? Explique.
7 - Walter está jogando um jogo com dois dados de 6 lados equiprováveis. O jogo consiste em lançar ambos os dados e caso a soma dos dados seja divisível por 3, ele ganhará, percendo em caso contrário. Realize um procedimento de MC para avaliar o jogo e responda a pergunta: Em média o jogo é favorável ao jogador?
8 - Suponha que tenhamos uma urna com bolas de mesmo tamanho enumeradas de 1 à 100. Considere o experimento aleatório de retirar uma bola da urna e observar o seu número até obtermos a bola com número desejado. Nesse experimento, será considerado reposição, isto é, caso não tenha sido observado a numeração desejada, a bola será devolvida à urna. Implemente um procedimento de MC considerando 10 mil repetições desse experimento e obtenha a média das retiradas necessárias para obter-se o número desejado. Além disso, retorne uma aproximação da probabilidade de se obter o número desejado. Dica: considere o número 77 como o número desejado.
9 - Um dono de cassino estuda disponibilizar um novo jogo e solicita uma consultoria estatística para saber se o jogo será viável para o cassino, isto é, se o valor esperado em dólares do lucro obtido será positivo, em média. Realize uma simulação de MC considerando 100 mil jogos e obtenha o valor médio de lançamentos de um jogador bem como a probabilidade (aproximada) de um jogador jogar apenas uma única partida. Além disso, responda: Se um jogador paga \(\$\) 10 dólares para jogar e lucra \(\$\) 1,50 dólares por cada jogada, o jogo é rentável para o dono do cassino?
Regras do Jogo:
Dois dados são lançados e caso a soma for 5, 6, 7, 8 ou 9 o jogo termina imediatamente;
Se nenhum dos resultamos acima for obtido, o jogador continua lançando ambos os dados até obter uma soma igual à 11 ou 12.
10 - Explique, com suas palavras, o que é paralelização multicore. Descreva brevemente os conceitos de nó, thread (hardware), processo master e trabalhadores.
11 - Descreva brevemente o sistema FORK e PSOCK. Apresente um exemplo de um código paralelizado usando o sistema FORK e PSOCK, respectivamente.
12 - Defina speedup e explique o significado.
13 - Ao paralelizar um algoritmo, teremos garantia da melhoria do desempenho computacional? Explique.
14 - Enuncie a Lei de Amdahl e cite um ponto negativo dessa lei. Qual o valor máximo de speedup definido por essa lei?
15 - Implemente um procedimento de MC, utilizando paralelismo para avaliar o cálculo do estimador de \(\hat{I}\) definido no exercício 3. Obtenha o speedup e discuta o resultado.
16 - Implemente uma versão paralela dos exercícios 5, 6, 7, 8 e 9. Avalie a implementação paralela com a versão serial. Houveram melhoria no desempenho computacional utilizando as versões paralelizadas? Explique.
17 - Implemente de forma paralela, uma função que realiza uma simulação de MC para avaliar o procedimento de MC para aproximação da constante \(\pi\). Obtenha o speedup e discuta o resultado. Considere 100 mil iterações em ambos os procedimentos.
18 - Implemente uma versão paralelizada do método da aceitação e rejeição para geração de números pseudo-aleatórios. Obtenha o speedup e discuta se houve ou não melhorias no desempenho computacional ao considerar-se a versão paralelizada. Explique.
6.5 Bootstrap
O método bootstrap foi introduzido em 1979 por Bradley Efron em um artigo publicado no The Annals of Statistics. A referência do artigo encontra-se abaixo e poderá ser acesso pelo link na referência, uma vez que o artigo é aberto.
Efron, B. Bootstrap methods: another look at the jackknife. The Annals of Statistics, v. 7, p. 1–26, 1979.
Tal método foi inspirado em uma metodologia anterior baseada em reamostragem denominada jackknife, idealizada por Maurice Quenouille em 1949 e aperfeiçoada em 1956. Para maiores detalhes, consulte as referências abaixo:
Quenouille, Maurice H. Problems in Plane Sampling. The Annals of Mathematical Statistics, v. 20, 355–375, 1949.
e
Quenouille, Maurice H. Notes on Bias in Estimation. Biometrika, v. 43, 353–360, 1956.
Efron sintetizou as metodologias baseadas em reamostragem que até então existiam e estabeleceu uma nova área de pesquisa. Pode-se dizer que o jackniffe é uma aproximação ou mesmo um caso particular do método bootstrap.

Figura 6.12: Bradley Efron, criador da técnica de reamostragem bootstrap amplamente utilizada na estatística e em outras áreas.
O termo bootstrap teve origem na obra literária do escritor alemão Rudolf Erich Raspe (1736–1794), mais precisamente de uma de suas óbras mais conhecidas intitulada The Surprising Adventures of Baron Munchausen, em que é dito:

“The Baron had fallen to the bottom of a deep lake. Just when it looked like all was lost, he thought to pick himself up by his own bootstraps.”
Tradução: “O Barão tinha caı́do no fundo de um lago profundo. Justo quando parecia que tudo estava perdido, ele pensou em retirar-se por seus próprios bootstraps.”).
Inicialmente houve ceticismo sobre a metodologia bootstrap, tendo sido tal ceticismo superado à medida em que estudos acumularam evidências de que o bootstrap pode ser consideravelmente mais eficaz que metodologias tradicionais.
A ideia de substituir aproximações complicadas e muitas vezes imprecisas por métodos de simulação baseados em reamostragem tem atraído diversos pesquisadores a desenvolver metodologias baseadas em bootstrap para os mais variados fins. Com a popularização do método bootstrap, alguns pesquisadores começaram a estabelecer condições matemáticas sob as quais o bootstrap é justificável.
Na literatura existem muitos trabalhos que fazem uso de metodologias bootstrap. Em geral, o método bootstrap é utilizado para correção de viés de estimadores, construção de intervalos de confiança, testes de hipóteses, estimação do erro-padrão de um estimador, entre outros.
As metodologias bootstrap apresentam dois paradigmas, sendo eles o bootstrap paramétrico e o bootstrap não-paramétrico. Bootstrap paramétrico refere-se ao caso em que a reamostragem é feita com base em uma distribuição \(F(\widehat{\theta})\) conhecida ou estabelecida, em que \(\widehat{\theta}\) é um estimador para \(\theta\). Em contrapartida, no bootstrap não-paramétrico há o desconhecimento da distribuição \(F\) verdadeira. A reamostragem é feita com base na função de distribuição empírica \(F_n\). Reamostrar de \(F_n\) equivale a reamostrar dos dados com reposição.
O bootstrap não-paramétrico trata a amostra como se fosse a população e a reamostragem é realizada dessa amostra como se estevessemos amostrando da população. O método de bootstrap não-paramétrico é frequentemente utilizado quando a distribuição da população alvo não é especificada. Nesse casos, temos apenas as informações contidas na amostra, em que poderemos fazer uso da distribuição empírica (distribuição dos dados) como uma aproximação da distribuição verdadeira \(F\) (desconhecida).
Seja \(\pmb X = (X_1, \ldots, X_n)\) uma sequência de v.a.’s i.i.d. (uma amostra aleatória), tal que \(F_{X_i}\) é desconhecida, com \(i = 1, \ldots, n\). Como a natureza funcional de \(F_{X_i}\) é desconhecida, as únicas informações que teremos a nossa disposição são as observações da amostra aleatória, ou seja, \(\pmb x = (x_1, \ldots, x_n)\). Muito embora desconhecemos \(F_{X_i}\), sabemos que
\[P\Big(\lim_{n\to \infty} \mathrm{sup}|F_n - F_{X_i}| = 0\Big) = 1,\] em que \(F_n\) é a função de distribuição empírica (função de distribuição dos dados) que é dada por:
\[F_n(t) = \frac{1}{n} \sum_{i = 1} ^ n I\{x_i \leq t\}.\] O resultado acima é conhecido como Teorema de Glivenko-Cantelli. Em outras palavras, o teorema afirma que \(F_n\) converge quase certamente para \(F_{X_i}\) (\(F_n \overset{q.c.}{\to} F_{X_i}\)). Para maiores detalhes, veja a página 336 do livro Probabilidade e Variáveis Aleatórias, Ed. 3, 2011 de Marcos N. Magalhães.
Exemplo: O código abaixo é responsável pela construção gráfica da distribuição empírica \(F_n\) com base em uma amostra. A função empirical() recebe como argumento observações de uma amostra aleatória e constrói o gráfico de \(F_n\). Após o código da função empirical() são gerados números pseudo-aleatórios (50 observações) provenientes de uma amostra aleatória com distribuição \(Weibull(\alpha = 1.5, \beta = 2.0)\) (distribuição verdadeira). A função empirical() irá graficar uma estimativa da distribuição \(Weibull(\alpha = 1.5, \beta = 2.0)\) por meio de \(F_n\) (em laranja), em que a curva preta é a distrbuição verdadeira, isto é, a distribuição \(Weibull(\alpha = 1.5, \beta = 2.0)\). Dica: Reproduza o código para diverentes tamanhos de amostra. Perceba que para valores grandes de amostra, por exemplo, 1000, 10000 ou 100000, o gráfico obtido de \(F_n\) se confunde com o gráfico de \(F\).
empirical <- function(x, ...){
domain <- seq(from = floor(min(x)), to = ceiling(max(x)) + 1L, length.out = 1e3L)
test <- function(i) sum(x <= domain[i]) / length(x)
prob <- purrr::map_dbl(.x = 1L:length(domain), .f = test)
plot.new()
plot.window(xlim = c(floor(min(x)), ceiling(max(x))), ylim = c(0, 1))
axis(1); axis(2)
lines(domain, prob, col = rgb(1, 0.5, 0.04), ...)
title(xlab = "x", ylab = "Probabilidade", main = paste("n = ", length(x)))
}
# Dados proveniente da distribuição verdadeira
# Weibull(alpha = 0.5, beta = 1.3):
set.seed(1L)
dados <- rweibull(50L, shape = 1.5, scale = 2.0)
# Construindo a função de distribuição empírica através dos dados:
empirical(dados, lwd = 3)
# Desenhando a função de distribuição teórica sobre o gráfico da
# função de distribuição empírica:
x <- seq(from = floor(min(dados)), to = ceiling(max(dados)), length.out = 1e3L)
lines(x = x, y = pweibull(q = x, shape = 1.5, scale = 2.0), lwd = 3)
# Acrescentando uma legenda:
legend(x = "right", legend = c(expression(F, F[n])), bty = "n",
lty = c(1, 1), lwd = c(3, 3), col = c("black", rgb(1, 0.5, 0.04)))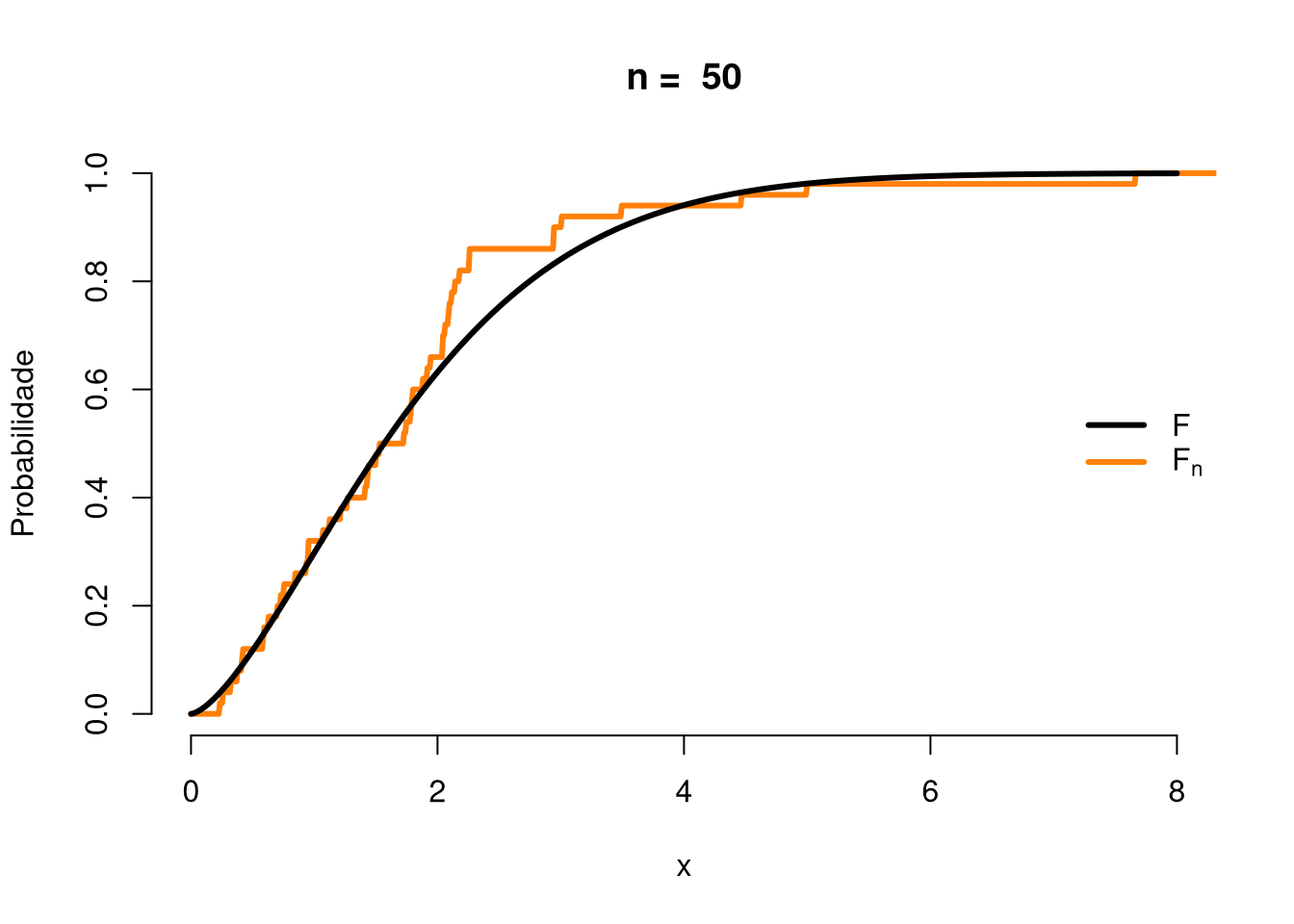
Figura 6.13: Função de distribuição empírica em azul versus a função de distribuição teórica em preto para um tamanho de amostra n = 50.
Em uma abordagem não-paramétrica, um histograma poderia ser uma estimativa gráfica da função de distribuição verdadeira, uma vez que para a construção do gráfico, utiliza-se \(\pmb x\). Em um bootstrap não-paramétrico, como dito anteriormente, uma amostra bootstrap é obtida por uma reamostragem (com reposição) de \(\pmb x\) e denotamos por \(\pmb x^*\), que são observações da amostra aleatória bootstrap \(\pmb X^* = (X^*_1, \ldots, X^*_n)\). Em outras palavras, reamostrar de \(\pmb x\) (com reposição) quer dizer que poderemos gerar uma amostra bootstrap tomando \(n\) valores inteiros \(\{i_1, \ldots, i_n\}\) uniformemente distribuídos em \(\{1, \ldots, n\}\) e selecionando \(\pmb x^* = (x_{i_1}, \ldots, x_{i_n})\). Isso quer dizer que para algum \(X^*_i\), seja ele denotado simplesmente por \(X^*\), tem-se:
\[P(X^* = x_i) = \frac{1}{n}, \, i = 1, \ldots, n.\] Sendo assim, note que a função de distribuição teórica de \(X^*\) é dada por \(F_n\). Daí, amostrar de \(\pmb x\) (com reposição) nos geram amostras bootstrap que tem a distribuição empírica como distribuição teórica e que sabemos que converge quase cetamente para \(F\) (desconhecida).
Seja \(T_n = \hat{\theta}\) um estimador de \(\theta\) com base na amostra aleatória original \(\pmb X\), em que \(\theta\) é um parâmetro ou vetor de parâmetros. Temos que \(t\) é a estimativa obtida por \(T_n\) com base nas observações originais \(\pmb x\). Analogamente, considere \(T_n^* = \hat{\theta}^*\) o mesmo estimador \(T_n\) sobre uma amostra aleatória bootstrap \(\pmb X^*\), em que \(t^*\) é a estimativa obtida por \(T_n^*\) com base em uma pseudo-amostra bootstrap \(\pmb x^*\).
Assim, uma estimativa da função de distribuição de \(T_n\) poderá ser obtida com os passos abaixo:
Para cada réplica bootstrap, \(b = 1, \ldots, B\):
Gere uma amostra bootstrap \(\pmb x^{*,b} = (x_1^*, \ldots, x_n^*)\) por reamostragem com reposição de \(\pmb x = (x_1, \ldots, x_n)\).
Obtenha a estimativa \(t^*\) com base em \(\pmb x^{*,b}\) gerada no passo anterior.
A estimativa bootstrap de \(F_{T_n}(\cdot)\) é a função de distribuição empírica das estimativas bootstrap \(t^{*,1}, \ldots, t^{*,B}\).
Exemplo: Suponha que \(T_n = \overline{X}\) e considere \(\pmb x = (x_1, \ldots, x_n)\) observações de uma amostra aleatória \(\pmb X = (X_1, \ldots, X_n)\), em que \(X_i \sim \mathrm{Exp}\Big(\lambda = \frac{1}{2}\Big)\), com \(i = 1, \ldots, n\), com \(n = 250\). Então, por meio do algoritmo acima, poderemos obter, com o código abaixo, uma estimativa da distribuição de \(T_n\). Nesse caso, não é difícil perceber que a distribuição de \(T_n\) terá distribuição \(\mathcal{N}(\mu, \sigma^2/n)\), em que \(\mu = \mathrm{E}(X) = 1/\lambda\) e \(\sigma^2 = \mathrm{Var}(X) = 1/\lambda^2\). Nesse caso, a distribuição teórica de \(T_n\) é \(\mathcal{N}(2, 0.016)\).
# Amostra original:
x <- rexp(250L, 0.5) # lambda = 1/2
bootstraping <- function(B = 100L, sample_true, stat, ...){
# A função resample() obtem uma amostra com reposição de x:
resample <- function(x){
n <- length(x)
# Selecionando observações uniformemente distribuídas em x.
# Poderia ser utilizado a função sample().
x[floor(n * runif(n = n, min = 0, max = 1) + 1L)]
}
# A função boot() calcula uma statística em uma única amostra
# bootstrap:
boot <- function(x, sample_true){
stat(resample(sample_true), ...)
}
purrr::map_dbl(.x = 1L:B, .f = boot, sample_true = sample_true)
# or
#lapply(X = 1L:N, FUN = boot, sample_true)
}
# Fixando uma semente:
set.seed(1L)
# Observe que stat é a média amostra, uma vez que passamos a função
# mean().
result <- bootstraping(B = 3e3L, sample_true = x, stat = mean)
hist(result, probability = TRUE, main = expression(paste("Aproximação para a densidade de ", T[n])),
border = NA, col = rgb(1, 0.9, 0.8), xlab = expression(t^"*"), ylab = "Probabilidade")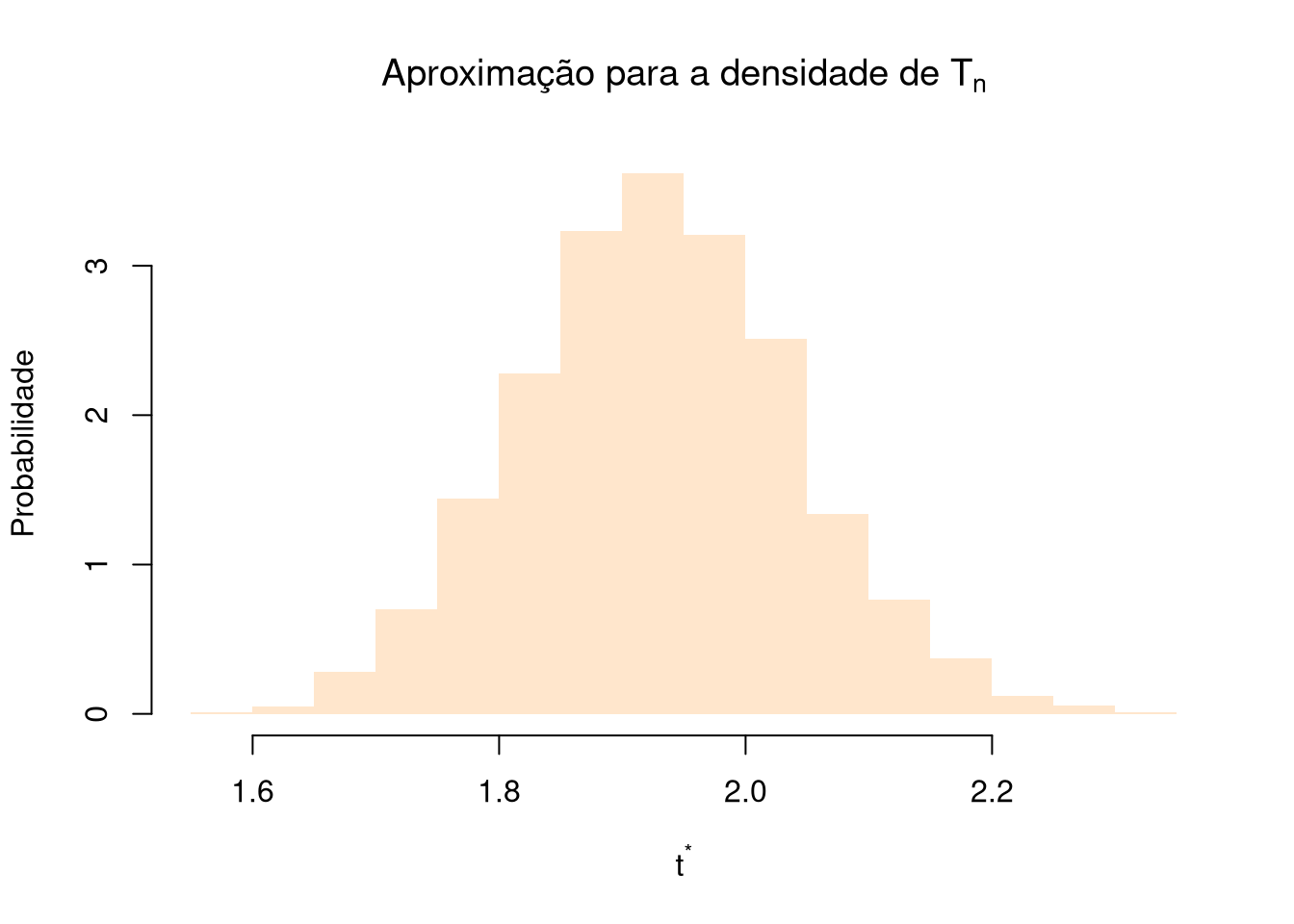
Figura 6.14: Histograma construído com base nas estimativas obtidas nas amostras bootstrap. Trata-se de uma aproximação para a densidade da estatística que nesse caso é a média amostral.
Importante:
O método de bootstrap não deverá ser utilizado para estimar \(\theta\). Por exemplo, \(1/B \sum_{i = 1}^B t_i^*\) pode não ser uma boa estimativa para \(\theta\). O bootstrap fornece boas aproximações para a forma e amplitude da distribuição de \(T_n\) mas não necessariamente para a sua locação. Isso se deve ao fato que temos duas fontes de erro, uma vez a função de distribuição empírica \(F_n^*\) obtida por \(\pmb x^*\) aproxima a distribuição teórica de \(X^*\) que é \(F_n\) e esta por sua vez aproxima \(F\) por meio de \(\pmb x\).
6.5.1 Estimando erro-padrão
A estimativa bootstrap para o erro-padrão de \(T_n\) poderá ser escrita como:
\[\widehat{se}(T_n)_{\mathrm{boot}} = \sqrt{\frac{1}{B-1}\sum_{i=1}^B(T_n^{*,i} - \overline{T_n^*})^2},\] em que \(\overline{T_n^*} = \frac{1}{B}\sum_{i=1}^B T^{*,i}\), sendo \(T_n^{*,i}\) o estimador \(T_n\) com base na \(i\)-ésima amostra bootstrap. Segundo Efron e Tibshirani, no livro B. Efron and R. J. Tibshirani. An Introduction to the Bootstrap. Chapman & Hall/CRC, Boca Raton, FL, 1993, p. 52, não é necessário um número de amostras bootstrap \(B\) muito grande. Segundos os autores, \(B = 50\) é um número suficientemente grande na maioria dos casos e \(B > 200\) é raramente necessário.
Nota:
Para obtenção de uma boa estimativa do erro-padrão de \(T_n\), considere \(B \geq 250\).
Exemplo: O código que segue calcula uma estimativa via bootstrap para o erro-padrão do estimador \(\overline{X} = n^{-1}\sum_1^n X_i\) de \(\mu\), com \(X_i, \ldots, X_n\) sendo amostra aleatória tal que \(X_i \sim \mathcal{N}(\mu = 0, \sigma^2 = 1)\). Note que a função bootstraping() implementada em exemplo anterior realiza a reamostragem por bootstrap não-paramétrico, mais precisamente mil amostras bootstrap (N = 1e3L) sobre uma amostra original (sample_true = amostra) e obtem sobre cada uma das amostras bootstrap uma estimativa da média amostral (stat = mean). Assim, fazer sd(bootstraping()) é calcular uma estimativa do erro-padrão de \(\overline{X}\) utilizando o estimador bootstrap \(\widehat{se}(T_n)_{\mathrm{boot}}\). Perceba que \(\sqrt{\mathrm{Var}(\overline{X})} = \sqrt{1/250}\) e que a estimativa bootstrap do erro-padrão de \(T_n = \overline{X}\) é bem aproximada por \(\widehat{se}(T_n)_{\mathrm{boot}}\).
# Fixando uma semente.
set.seed(1L)
# O objeto "amostra" é a amostral original.
amostra <- rnorm(n = 250L, mean = 0, sd = 1) # Amostra original.
# Obtendo mil amostras bootstrap com reposição da amostra original e calcuando
# a média amostral, i.e, T_n^* é a média amostral (stat = mean). Note que fazer
# var(bootstraping()) estamos obtendo uma estimativa do erro-padrão via bootstrap
# da média amostral.
sd(bootstraping(N = 1e3L, sample_true = amostra, stat = mean))## [1] 0.06307263Impotante:
A amostra original não precisa ser observações de v.a.’s com distribuição normal. Utilizamos o caso da normal para facilitar as contas. O método bootstrap poderá ser aplicado à observações de uma amostra aleatória com distribuição qualquer.
6.5.2 Diminuindo o viés
Se \(T_n\) é um estimador não-viesado para \(\theta\), então \(\mathrm{E}(T_n) = \theta\). Porém, alguns estimadores podem ser viesados para estimar \(\theta\), em que o seu viés poderá ser obtido por:
\[B(T_n) = \mathrm{E}(T_n - \theta) = \mathrm{E}(T_n) - \theta.\] Diremos que um \(T_n\) é um estimador assintoticamente não-viesado para \(\theta\) se \(\lim_{n \to \infty} B(T_n) = 0\). Alguns estimadores podem ter boas propriedades estatísticas mas serem viesados em amostras que não são suficientemente grandes. Por exemplo, os estimadores de máxima veorssimilhança podem ser viesados em pequenas amostras mas sabemos que são assintoticamente não-viesados, como é o caso do estimador de máxima verossimilhança de \(\sigma^2\) dado por \(\hat{\sigma}^2 = 1/n \sum_{i=1}^{n}(X_i - \overline{X})^2\), com \(X_i, \ldots, X_n\) sendo uma amostra aleatória tal que \(X_i \sim \mathcal{N}(\mu, \sigma^2)\), com \(i = 1, \ldots, n\). Nesse caso, \(\mathrm{E}(\hat{\sigma}^2) = \frac{(n-1)}{n} \sigma^2\). Daí, poderemos corrigir o víes de \(\hat{\sigma}^2\) considerando \(S^2 = \frac{n}{n-1}\hat{\sigma}^2 = \frac{1}{n-1} \sum_{i=1}^{n}(X_i - \overline{X})^2\). Em um situação ideal, temos que o estimador \(T_n\) corrigido por víes é dado por
\[T_n^{\mathrm{ideal}} = T_n - B(T_n).\] Porém, note que \(T_n^{\mathrm{ideal}}\) não é um estimador, uma vez que \(T_n^{\mathrm{ideal}}\) depende de \(\theta\). Assim, em uma situação quase-ideal, temos que
\[T_n^{\mathrm{quase-ideal}} = T_n - \widehat{B(T_n)}.\]
Queremos construir um estimador \(T_n^{\mathrm{corrigido}}\) semelhante à \(T_n^{\mathrm{quase-ideal}}\).
\[T_n^{\mathrm{corrigido}} = T_n - \widehat{B(T_n)} = T_n - [\widehat{\mathrm{E}(T_n)} - T_n] = 2T_n - \widehat{\mathrm{E}(T_n)}.\]
O estimador bootstrap do viés utiliza-se, assim como em qualquer método bootstrap, a distribuição bootstrap de \(T_n\) para estimar a distribuição de \(T_n\). Assim, tome
\[\widehat{\mathrm{E}(T_n)} = \frac{1}{n}\sum_{i=1}^B T_n^{*,i} = \overline{T_n^{*}}.\] Portanto, o estimador \(T_n\) corrigido por bootstrap é dado por:
\[T_n^{\mathrm{corrigido-boot}} = 2T_n - \overline{T_n^{*}}.\]
Dessa forma, a estimativa corrigida por bootstrap é dada por \(t_n^{\mathrm{corrigido-boot}} = 2t_n - \overline{t_n^*}\), em que \(t_n\) é a estimativa obtida por \(T_n\) em \(\pmb x\) e \(\overline{t_n^*}\) é a média das estimatativas obtidas por \(T_n\) calculada sobre as amostras bootstrap \(\Big(t_n^{*,1},\ldots, t_n^{*,B}\Big)\). Sendo assim, \(t_n^{\mathrm{corrigido-boot}}\) dará a estimativa para \(\theta\) corrigida por bootstrap.
Exemplo: Implemente a função bias_boot(B = 100L, sample_true, f, kicks, idpar = 1L, ...) que receberá como argumentos a quantidade de réplicas bootstrap (B), a amostra original (sample_true), uma f.d.p / f.p (f) ao qual obteremos as estimativas de máxima verossimilhança por métodos númericos, os chutes iniciais kicks utilizado pelo método de minimização de \(-\mathcal{l}(\pmb \theta)\), em que \(\mathcal{l}(\pmb \theta)\) é a função de log-verossimilhança e \(\pmb \theta\) é o vetor de parâmetros que idexam a f.d.p / f.p. Os dois últimos argumentos idpar = 1L e ... informa o parâmetro ao qual desejamos corrigir por viés via bootstrap, em que 1L indica o primeiro parâmetro de \(\pmb \theta\) e argumentos adicionais passados à função de otimização optim(), respectivamente. A ideia é que bias_boot() é que seja uma função que receba, por exemplo, uma f.d.p e retorne a estimativa de máxima verossimilhança sobre a amostra original e a estimativa corrigida por bootstrap. Por exemplo, se é \(X_1, \ldots, X_n\) uma sequência de v.a.’s i.i.d (amostra aleatória), tal que \(X_i \sim Weibull(\alpha = 2, \beta = 2)\), para \(i = 1, \ldots, n\), então
amostra <- rweibull(n = 30L, shape = 2, scale = 2)
bias_boot(B = 500L, sample_true = amostra, f = fdp_weibull,
kicks = c(1, 1), idpar = 1L, method = "BFGS")deverá retornar a estimativa de máxima verossimilhança de \(\alpha\) e a respectiva estimativa corrigida por viés via bootstrap. O trecho acima, temos que 500 réplicas bootstrap, um objeto amostra com a amostra original, fdp_weibull() a função densidade de uma v.a. com distribuição Weibull, os chutes iniciais \(\alpha_0 = 1\) e \(\beta_0 = 1\) para o método BFGS. O argumento idpar = 1L indica que desejamos corrigir por viés, via bootstrap, o parâmetro \(\alpha\) que fixamos em 2.
bootstraping <- function(B = 100L, sample_true, f, kicks, idpar = 1L, ...){
log_likelihood <- function(par, x){
-sum(log(f(par, x)))
}
# A função resample() obtem uma amostra com reposição de x:
resample <- function(x) {
n <- length(x)
# Selecionando observações uniformemente distribuídas em x.
# Poderia ser utilizado a função sample().
x[floor(n * runif(n = n, min = 0, max = 1) + 1L)]
} # Aqui termina a função resample().
# A função boot() calcula uma statística em uma única amostra
# bootstrap:
boot <- function(i) {
#result <- double(1L)
repeat {
result <- optim(par = kicks, fn = log_likelihood, x = resample(sample_true), ...)
if (result$convergence == 0L) {
result <- result$par[idpar]
break
}
}
result
} # Aqui termina a função boot().
purrr::map_dbl(.x = 1L:B, .f = boot)
}Descervendo melhor a função bootstraping() acima:
O código acima apresenta uma nova implementação da função bootstraping() de forma que, agora, a função irá obter as estimativas de máxima verossimilhança utilizando métodos numéricos. Sendo assim, bootstraping() irá receber como argumento o número de réplicas bootstrap (B), a amostra original (sample_true), uma f.d.p / f.p (f), os chutes iniciais (kicks) para o método iterativo utilizado para minimizar \(-\mathcal{l(\pmb \theta)}\), em que \(\mathcal{l}(\cdot)\) é a função de log-verossimilhança e \(\theta\) é o vetor de parâmetros que indexa a função f.d.p / f.p passada como argumento à f. O argumento idpar = 1L refere-se à posição do parâmetro que desejamos efetuar a correção de viés via bootstrap (por padrão é o primeiro) do vetor \(\pmb \theta\). O argumento ... irá permitir que argumentos adicionais sejam passados à função bootstraping() e aplicados à função optim() utilizada para obtenção das estimativas numéricas. Por exemplo, poderemos passar method = "BFGS" à bootstraping() que é um argumento suportado pela função optim().
Assim como na implementação anterior da função bootstraping(), no exemplo logo acima, temos que resample() é uma função simples que é resposável por reamostrar com reposição da amostra original passada à sample_true(). A função resample() é utilizada dentro da função boot(). A função boot() obtem as estimativas numéricas de máxima verossimilhaça sobre uma amostra bootstrap. Perceba que utiliza-se a estrutura de repetição repeat para repetir o processo de optimização sobre outra amostras bootstrap, caso não haja convergência do método de otimização, uma vez que result$convergence diferente de zero indica não convergência do método iterativo de minimização. Não haver convergência sobre uma dada amostra bootstrap implica que as estimativas obtidas não são estimativas de máxima verossimilhança. Precisamos que \(T_n^*\) sejam estimativas de máxima veorissmilhança, o que convêm substituir uma amostra que não houve convergência por outra amostra em que a convergência é observada.
No código abaixo é implementado a função fdp_weibull() que sejá passado como argumento para a função bias_boot() que é responsável por corrigir por viés, via bootstrap, a estimativa de máxima verossimilhança de um dos parâmetros que indexa fdp_weibull(). Por padrão, o argumento é o primeiro, isto é, idpar = 1L. Perceba que a função bias_boot() faz uso da função bootstraping() que é responsável por fazer todo o trabalho pesado. Ao final, bias_boot() retornará uma lista com a estimativa de máxima verossimilhança sem correção e a restivativa corrigida por viés, via bootstrap, respectivamente.
# Função densidade da Weibull:
fdp_weibull <- function(par, x){
alpha <- par[1]
beta <- par[2]
dweibull(x, shape = alpha, scale = beta)
}
bias_boot <- function(B = 100L, sample_true, f, kicks, idpar = 1L, ...){
log_likelihood <- function(par, x){
-sum(log(f(par, x)))
}
result <- optim(par = kicks, fn = log_likelihood, x = sample_true, ...)$par[idpar]
result_boot <- 2 * result - mean(bootstraping(B, sample_true, f, kicks, idpar, ...))
list(stat = result, stat_corrigida = result_boot)
}
set.seed(1L) # Fixando uma semente.
# O objeto "amostra" é a amostral original.
amostra <- rweibull(n = 30L, shape = 2, scale = 2)
bias_boot(B = 500L, sample_true = amostra, f = fdp_weibull,
kicks = c(1, 1), idpar = 1L, method = "BFGS")## $stat
## [1] 2.221581
##
## $stat_corrigida
## [1] 2.064491Observe que a estimativa corrigida por bootstrap fornece uma melhor estimativa para o parâmetro \(\alpha = 2.\)
Nota:
Segundo Efron e Tibshirani, no livro B. Efron and R. J. Tibshirani. An Introduction to the Bootstrap. Chapman & Hall/CRC, Boca Raton, FL, 1993, p. 129, se
\[\frac{|\widehat{B(T_n)}|}{\widehat{se}(T_n)_{\mathrm{boot}}} \leq 0.25,\] em que \(\widehat{B(T_n)}\) é o viés do estimador \(T_n\) estimado por bootstrap, a correção por viés via bootstrap poderá não ser necessária.
Exemplo: O exemplo abaixo mostra como incorporar uma barra de progresso (usando caracteres ASCII) que informará o quão próximo estamos do fim da execução da função bias_boot(). Note a execução repetida de boot(), implementada dentro do escopo da função bootstraping() é o que verdadeiramente torna custosa a execução da função bias_boot(). Dessa forma, escolheu-se dentro de boot() atualizar o progresso usando o comando pb$tick(). Perceba que antes da definição de boot() foi criado o objeto pb da classe progress_bar, em que foi informado o número total de chamadas à boot(). Perceba que é necessário instalar o pacote progress que está disponível nos repositórios do CRAN. Note também que foram utilizadas as funções tic() e toc() do pacote tictoc como uma alternativa para marcar o tempo de execução da função bias_boot(). Trata-se de uma alternativa à função system.time() do pacote base.
library(progress)
bootstraping <- function(B = 100L, sample_true, f, kicks, idpar = 1L, ...){
log_likelihood <- function(par, x){
-sum(log(f(par, x)))
}
# A função resample() obtem uma amostra com reposição de x:
resample <- function(x) {
n <- length(x)
# Selecionando observações uniformemente distribuídas em x.
# Poderia ser utilizado a função sample().
x[floor(n * runif(n = n, min = 0, max = 1) + 1L)]
} # Aqui termina a função resample().
# A função boot() calcula uma statística em uma única amostra
# bootstrap:
pb <- progress_bar$new(total = B) # objeto progress_bar.
boot <- function(i) {
#result <- double(1L)
repeat {
result <- optim(par = kicks, fn = log_likelihood, x = resample(sample_true), ...)
if (result$convergence == 0L) {
result <- result$par[idpar]
break
}
}
pb$tick() # Dando um tick().
result
} # Aqui termina a função boot().
purrr::map_dbl(.x = 1L:B, .f = boot)
}
set.seed(1L) # Fixando uma semente.
# O objeto "amostra" é a amostral original.
amostra <- rweibull(n = 30L, shape = 2, scale = 2)
tictoc::tic()
bias_boot(B = 2e3L, sample_true = amostra, f = fdp_weibull,
kicks = c(1, 1), idpar = 1L, method = "BFGS")
tictoc::toc()Nota:
O uso de uma barra informativa sobre o status da execução de uma função poderá adicionar custos computacionais.
6.5.3 Construindo intervalos aleatórios
Um intervalo de confiança (IC) é uma estimativa intervalar para um parâmetro de interesse de uma população. Em vez de estimar o parâmetro por um único valor (estimativa pontual), o intervalo de confiança fornece um conjunto de estimativas possíveis para esse parâmetro de interesse através de um intervalo aleatório. Estimativas intervalares são realizadas sob um nível de confiança \(1-\alpha\), com \(\alpha \in (0,1)\), em que \(\alpha\) é o nível de significância adotado e fixado pelo pesquisador. Um intervalo \(I_{\gamma}\) (intervalo de nível \(\gamma\)) para o parâmetro \(\theta\) é tal que \[\begin{equation} P(I_\gamma\,\, \mathrm{conter}\,\, \theta) = \gamma. \end{equation}\]
Um intervalo de confiança bilateral é delimitado pelos limites inferior e superior \(\ell_{\frac{\alpha_1}{2}}\) e \(\ell_{1-\frac{\alpha_2}{2}}\) respectivamente, em que, \(\alpha_1\) e \(\alpha_2\) pertencem ao conjunto de valores possíveis de \(\alpha\), tal que \[\begin{equation} P\left(\theta < \ell_{\frac{\alpha_1}{2}}\right) = \frac{\alpha_1}{2}\,\,\,\, \mathrm{e}\,\,\,\, P\left(\theta < \ell_{1-\frac{\alpha_2}{2}} \right) = 1 - \frac{\alpha_2}{2}. \end{equation}\]
A cobertura do intervalo \(\left[\ell_{\alpha_1/2},\ell_{1-\alpha_2/2}\right]\) é \(\gamma = 1 - (\frac{\alpha_1}{2}+\frac{\alpha_2}{2})\), com \(\alpha_1/2+\alpha_2/2 = \alpha\), sendo \(\alpha_1/2\) e \(\alpha_2/2\) os erros de coberturas à esquerda e à direta do intervalo \(I_\gamma\), respectivamente. As escolhas de \(\alpha_1\) e \(\alpha_2\) devem ser feitas de forma que a amplitude de \(I_{\gamma}\) seja a menor possível. Na prática é usual escolher \(\alpha_1\) e \(\alpha_2\) de modo que \[P\left(\theta < \ell_{\frac{\alpha_1}{2}}\right) = P\left(\theta > \ell_{1-\frac{\alpha_2}{2}}\right) = \frac{\alpha}{2}.\]
Uma abordagem frequentemente utilizada na construção de intervalos de confiança paramétricos é considerar um estimador \(\widehat{\theta}\) para um parâmetro \(\theta\) da população, em que \(\widehat{\theta}\) é usualmente um estimador de máxima verossimilhança de \(\theta\). Queremos encontrar um intervalo que contenha \(\theta\) com \(100\gamma\%\) de confiança. Seja \(T_n\) um estimador do escalar \(\theta\) baseado em \(n\) observações e \(t\) sua estimativa. Por simplicidade, suponhamos que \(T_n\) seja uma variável aleatória contínua. Denotando-se o \(p\)-ésimo quantil da distribuição da variável aleatória \(T_n - \theta\) por \(a_p\), temos que \[\begin{equation}\label{eq:ic_parametrico} P\left(T_n - \theta \leq a_{\frac{\alpha_1}{2}}\right) = \frac{\alpha}{2} = P\left(T_n - \theta \geq a_{1-\frac{\alpha_2}{2}}\right). \end{equation}\]
Como a quantidade \(Q = T_n - \theta\) é inversível em \(\theta\) e \(T_n\) depende apenas da amostra, podemos construir o intervalo de confiança para \(\theta\) reescrevendo os eventos, ou seja, podemos reescrever os eventos \(T_n -\theta \leq a_{\frac{\alpha_1}{2}}\) e \(T_n - \theta \geq a_{1-\frac{\alpha_2}{2}}\) como \(\theta > T_n - a_{\frac{\alpha_1}{2}}\) e \(\theta < T_n - a_{1-\frac{\alpha_2}{2}}\), respectivamente. Assim, o intervalo de confiança de nível \(\gamma\) é dado pelos limites \[\begin{equation}\label{eq:limites_de_confiancas} \ell_{\alpha/2} = t - a_{1-\frac{\alpha_2}{2}}, \, \, \ell_{1-\alpha/2} = t - a_{\frac{\alpha_1}{2}}. \end{equation}\]
Em situações em que o intervalo bilateral é de interesse, a soma de \(\alpha_1/2\) e \(\alpha_2/2\) é igual a \(\alpha\). Quando estamos interessados em intervalos simétricos, temos que \(\alpha_1 = \alpha_2 = \alpha\). Assim, a “forma geral” de um intervalo de confiança para um parâmetro \(\theta\) é:
\[\begin{equation}\label{eq:ic_geral} \ell_{\alpha/2} = t - a_{1-\alpha/2}, \, \, \ell_{1-\alpha/2} = t - a_{\alpha/2}. \end{equation}\]
Para os casos em que apenas um dos limites é de interesse, ou seja, o pesquisador está interessado na construção de intervalos de confiança unilaterais, temos que os limites para construção dos intervalos unilateral inferior e unilateral superior são dados por \(\ell_{1-\alpha}\) e \(\ell_{\alpha}\) respectivamente. Os limites serão obtidos de tal forma que \(P\left(\theta < \ell_{\alpha}\right) = P\left(\theta > \ell_{1-\alpha}\right) = \alpha\).
6.5.3.1 Bootstrap Percentil
Davison, A. C. e Hinkley, D. V, em Bootstrap methods and their application, Vol. 1, Cambridge university press, p. 202, (1997) afirma que existe alguma transformação de \(T_n\), \(U = h(T_n)\), tal que \(U\) possui uma distribuição simétrica. Suponhamos que sabemos calcular o intervalo de confiança de nível \(1-\alpha\) para \(\phi = h(\theta)\). Segundo Davison, A. C. e Hinkley, D. V (1997), podemos utilizar bootstrap para obter uma aproximação da distribuição de \(T_n-\theta\) utilizando a distribuição de \(T_n^* - t\). Dessa forma, estimamos o \(p\)-ésimo quantil de \(T_n-\theta\) pelo \((B+1)p\)-ésimo valor ordenado de \(t^* - t\), ou seja, o \(p\)-ésimo quantil de \(T_n-\theta\) é estimado por \(t_{((B+1)p)}^*-t\). Analogamente, o \(p\)-ésimo quantil de \(h(T_n)-h(\theta) = U - \phi\) poderá ser estimado pelo \((B+1)p\)-ésimo valor ordenado de \(h(T_n^*)-h(t) = u^* - u\). Seja \(b_p\) o \(p\)-ésimo quantil de \(U-\phi\). Como \(U\) tem distribuição simétrica, então \(U-\phi\) também tem distribuição simétrica, logo é verdade que \(b_\frac{\alpha}{2} = - b_{1-\frac{\alpha}{2}}\). Utilizando a forma geral para intervalos de confiança e a simetria de \(U-\phi\), temos que \(h(\ell_{\alpha/2}) = u+b_{\alpha/2}\) e \(h(\ell_{1-\alpha/2}) = u + b_{1-\alpha/2}\). Como \(b_{\alpha/2}\) e \(b_{1-\alpha/2}\) são quantis da distribuição de \(U-\phi\) e sabemos calcular os quantis dessa distribuição, temos que os limites inferior e superior de confiança são dados por \(u + (u_{((B+1)\alpha/2)}^* - u)\) e \(u + (u_{((B+1)(1-\alpha/2))}^* - u)\), respectivamente, implicando os limites
\[u_{((B+1)\alpha/2)}^*, \,\,\,\, u_{((B+1)(1-\alpha/2))}^*,\] cuja transformação para \(\theta\) é
\[t_{(B+1)\alpha/2}^{*}, \,\,\,\, t_{(B+1)(1-\alpha/2)}^{*}.\]
Observe que não precisamos conhecer a transformação \(h\). O intervalo de nível \(1-\alpha\) para o parâmetro \(\theta\) não envolve \(h\) e pode ser calculado sem o conhecimento desta transformação. O intervalo acima é conhecido como intervalo bootstrap percentil. Segundo Davison, A. C. & Hinkley (1997), p. 203, o método percentil poderá ser aplicado a qualquer estatística.
Nota:
Segundo B. Efron and R. J. Tibshirani. An Introduction to the Bootstrap. Chapman & Hall/CRC, Boca Raton, FL, 1993, p. 160, se \((B+1)\alpha/2\) não é inteiro, devemos considerar como limite inferior, o valor na posição \(\lfloor(B+1)\alpha/2\rfloor\) do vetor ordenado \(t_1^*, \ldots, t_B^*\), em que \(\lfloor\,\, x \,\,\rfloor\) é a parte inteira de \(x\), isto é,
\[\lfloor\,\, x \,\,\rfloor = \max\{n \in \mathbb{Z}\, :\, n \leq x\}.\]
Como limite superior do intervalo, tome o valor na posição \((B + 1 - k)\) do vetor ordenado. No R, utilize a função quantile() para obter os quantis desejados do vetor \(t_1^*, \ldots, t_B^*\).
Exercício
Defina função de distribuição empírica \(F_n(\cdot)\). Implemente a função
empirical(data, t)que recebe como argumento um conjunto de dados passado como argumento àdatae retorna \(F_n(t)\).Descreva, com poucas palavras, o método de reamostragem bootstrap e cite a diferença do bootstrap paramétrico para o bootstrap paramétrico. Explique.
Explique o porquê reamostramos com reposição de \(\pmb x = (x_1, \ldots, x_n)\), em que \(\pmb x\) é a amostra original, quando estamos fazendo uso de bootstrap não-paramétrico.
Seja \(\pmb X^* = (X_1^*, X_2^*, \ldots, X_n^*)\) uma amostra aleatória bootstrap. Qual a distribuição teórica de \(X_i^*\), com \(i = 1, \ldots, n\)? Explique.
Seja \(T_n\) um estimador qualquer. Defina o estimador bootstrap para obtenção da estimativa do erro-padrão de \(T_n\).
Defina o que o viés de um estimador \(T_n\) qualquer e denote por \(B(T_n)\). Como podemos utilizar o método bootstrap para obtenção da estimativa do viés de \(T_n\) via bootstrap? Explique.
O estimador \(T_n\) corrigido por viés via bootstrap é dado por \(T_n^{\mathrm{corrigido-boot}} = 2T_n - \overline{T_n^{*}}\). Explique como essa correção é obtida.
Suponha que \(T_n = \overline{X}\) e considere \(\pmb x = (x_1, \ldots, x_n)\) observações de uma amostra aleatória \(\pmb X = (X_1, \ldots, X_n)\), em que \(X_i \sim \mathrm{Exp}\Big(\lambda = \frac{1}{2}\Big)\), com \(i = 1, \ldots, n\). Para \(n = 50\), construa uma simulação de MC par avaliar \(\widehat{se}(T_n)_{\mathrm{boot}}\) e \(\widehat{B(T_n)}_{\mathrm{boot}}\). Discuta o resultado. Dica: considere 100 mil réplicas de MC e ao final obtenha a média das estimativas de \(\widehat{se}(T_n)_{\mathrm{boot}}\) e \(\widehat{B(T_n)}_{\mathrm{boot}}\).
Implemente o exercício anteiror de forma paralela. Obtenha o speedup.
Defina o método bootstrap percentil para obtenção de um intervalo aleatório para um parâmetro.
Implemente a função
percentile_boot(B = 250L, fun, alpha = 0.05, ...)que obtém um intervalo aleatório para algum parâmetro que indexa uma função densidade de probabilidade passada como argumento àfun, sendoBa quantidade de réplicas bootstrap considerada (padrão 250) e \(\alpha\) o nível de significância adotado (padrãoalpha = 0.05). Considere \(\widehat{T_n}\) a estimativa de máxima verossimilhança do parâmetro ao qual se deseja construir o intervalo. Dicas: [1] as estimativas \(t\) obtida por \(\widehat{T_n}\) são construídas de forma numérica. Assim, você terá que minimizar \(-\mathcal{l}(\theta)\) usando a funçãooptim(), em que \(\mathcal{l}(\theta)\) é a função de log-verossimilhança. [2] Considere o método BFGS. [3] Lembre-se de descartar as amostras bootstrap em que não houveram convergência do método BFGS. Substituia essas amostras por outra em que a convergência poderá ser observada.