Acceptance-Rejection Method

This function implements the acceptance-rejection method for generating random numbers from a given probability density function (pdf).

Usage

acceptance_rejection(
  n = 1L,
  continuous = TRUE,
  f = dweibull,
  args_pdf = list(shape = 1, scale = 1),
  xlim = c(0, 100),
  c = NULL,
  linesearch_algorithm = "LBFGS_LINESEARCH_BACKTRACKING_ARMIJO",
  max_iterations = 1000L,
  epsilon = 1e-06,
  start_c = 25,
  parallel = FALSE,
  ...
)

Arguments

n

The number of random numbers to generate.

continuous

A logical value indicating whether the pdf is continuous or discrete. Default is TRUE.

f

The probability density function (continuous = TRUE), in the continuous case or the probability mass function, in the discrete case (continuous = FALSE).

args_pdf

A list of arguments to be passed to the pdf function.

xlim

A vector specifying the range of values for the random numbers in the form c(min, max). Default is c(0, 100).

c

A constant value used in the acceptance-rejection method. If NULL, it will be estimated using the lbfgs::lbfgs() optimization algorithm. Default is NULL.

linesearch_algorithm

The linesearch algorithm to be used in the lbfgs::lbfgs() optimization. Default is "LBFGS_LINESEARCH_BACKTRACKING_ARMIJO".

max_iterations

The maximum number of iterations for the lbfgs::lbfgs() optimization. Default is 1000.

epsilon

The convergence criterion for the lbfgs::lbfgs() optimization. Default is 1e-6.

start_c

The initial value for the constant c in the lbfgs::lbfgs() optimization. Default is 25.

parallel

A logical value indicating whether to use parallel processing for generating random numbers. Default is FALSE.

...

Additional arguments to be passed to the lbfgs::lbfgs() optimization algorithm. For details, see lbfgs::lbfgs().

Value

A vector of random numbers generated using the acceptance-rejection method.

Details

In situations where we cannot use the inversion method (situations where it is not possible to obtain the quantile function) and we do not know a transformation that involves a random variable from which we can generate observations, we can use the acceptance and rejection method. Suppose that \(X\) and \(Y\) are random variables with probability density function (pdf) or probability function (pf) \(f\) and \(g\), respectively. In addition, suppose that there is a constant \(c\) such that

$$f(x) \leq c \cdot g(x), \quad \forall x \in \mathbb{R}.$$

for all values of \(t\), with \(f(t)>0\). To use the acceptance and rejection method to generate observations from the random variable \(X\), using the algorithm below, first find a random variable \(Y\) with pdf or pf \(g\), that satisfies the above condition.

Algorithm of the Acceptance and Rejection Method:

1 - Generate an observation \(y\) from a random variable \(Y\) with pdf/pf \(g\);

2 - Generate an observation \(u\) from a random variable \(U\sim \mathcal{U} (0, 1)\);

3 - If \(u < \frac{f(y)}{cg(y)}\) accept \(x = y\); otherwise reject \(y\) as an observation of the random variable \(X\) and return to step 1.

Proof: Let's consider the discrete case, that is, \(X\) and \(Y\) are random variables with pf's \(f\) and \(g\), respectively. By step 3 of the above algorithm, we have that \({accept} = {x = y} = u < \frac{f(y)}{cg(y)}\). That is,

\(P(accept | Y = y) = \frac{P(accept \cap {Y = y})}{g(y)} = \frac{P(U \leq f(y)/cg(y)) \times g(y)}{g(y)} = \frac{f(y)}{cg(y)}.\)

Hence, by the Total Probability Theorem, we have that:

\(P(accept) = \sum_y P(accept|Y=y)\times P(Y=y) = \sum_y \frac{f(y)}{cg(y)}\times g(y) = \frac{1}{c}.\)

Therefore, by the acceptance and rejection method we accept the occurrence of $Y$ as being an occurrence of \(X\) with probability \(1/c\). In addition, by Bayes' Theorem, we have that

\(P(Y = y | accept) = \frac{P(accept|Y = y)\times g(y)}{P(accept)} = \frac{[f(y)/cg(y)] \times g(y)}{1/c} = f(y).\)

The result above shows that accepting \(x = y\) by the procedure of the algorithm is equivalent to accepting a value from \(X\) that has pf \(f\).

The argument c = NULL is the default. Thus, the function acceptance_rejection() estimates the value of c using the optimization algorithm lbfgs::lbfgs(). For more details, see lbfgs::lbfgs(). If a value of c is provided, the function acceptance_rejection() will use this value to generate the random observations. An inappropriate choice of c can lead to low efficiency of the acceptance and rejection method.

In Unix-based operating systems, the function acceptance_rejection() can be executed in parallel. To do this, simply set the argument parallel = TRUE. The function acceptance_rejection() utilizes the parallel::mclapply() function to execute the acceptance and rejection method in parallel. On Windows operating systems, the code will be seral even if parallel = TRUE is set.

See also

parallel::mclapply() and lbfgs::lbfgs().

Examples

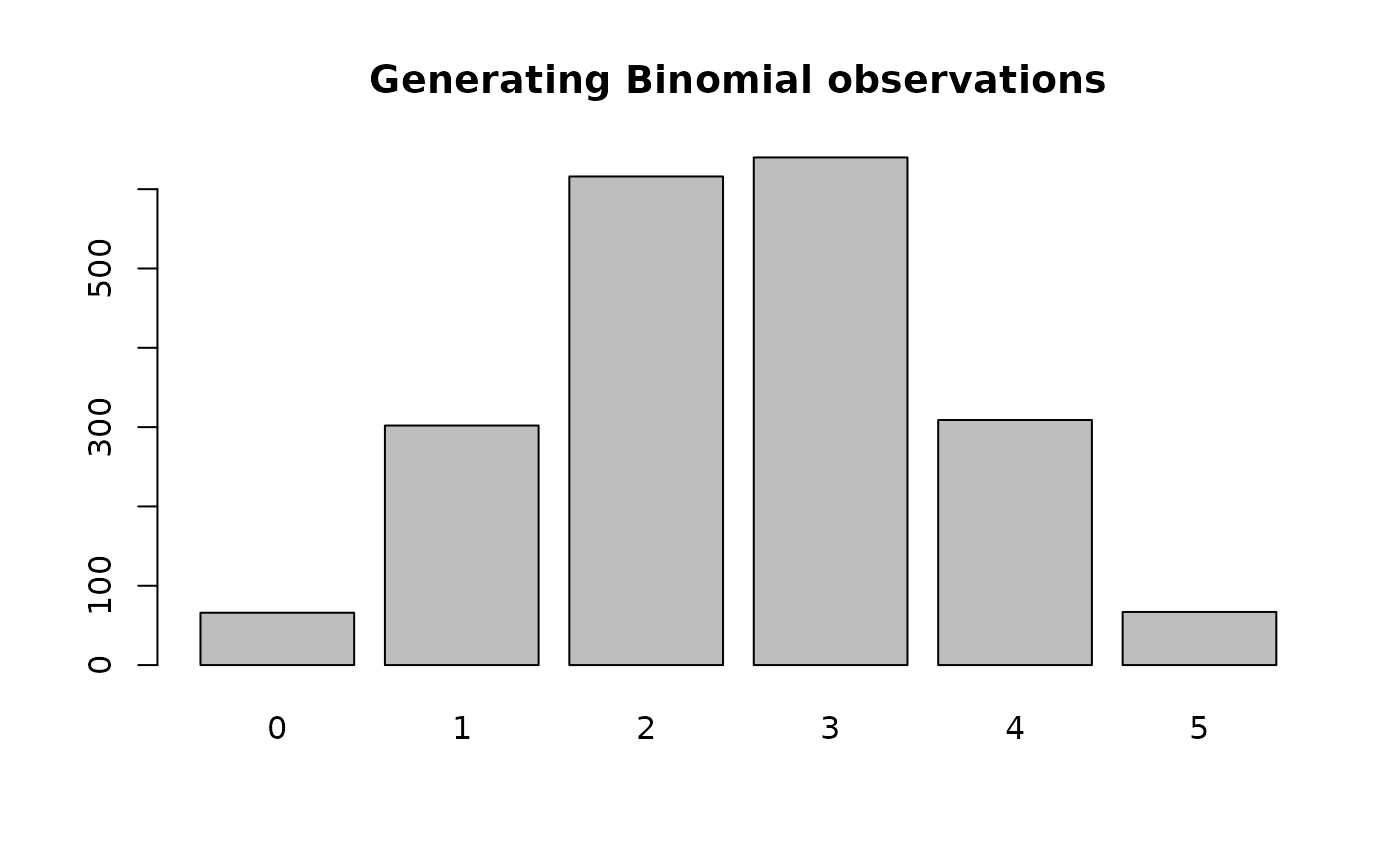
set.seed(0) # setting a seed for reproducibility

acceptance_rejection(
 n = 2000L,
 f = dbinom,
 continuous = FALSE,
 args_pdf = list(size = 5, prob = 0.5),
 xlim = c(0, 10)
) |>
table() |>
barplot(main = "Generating Binomial observations")


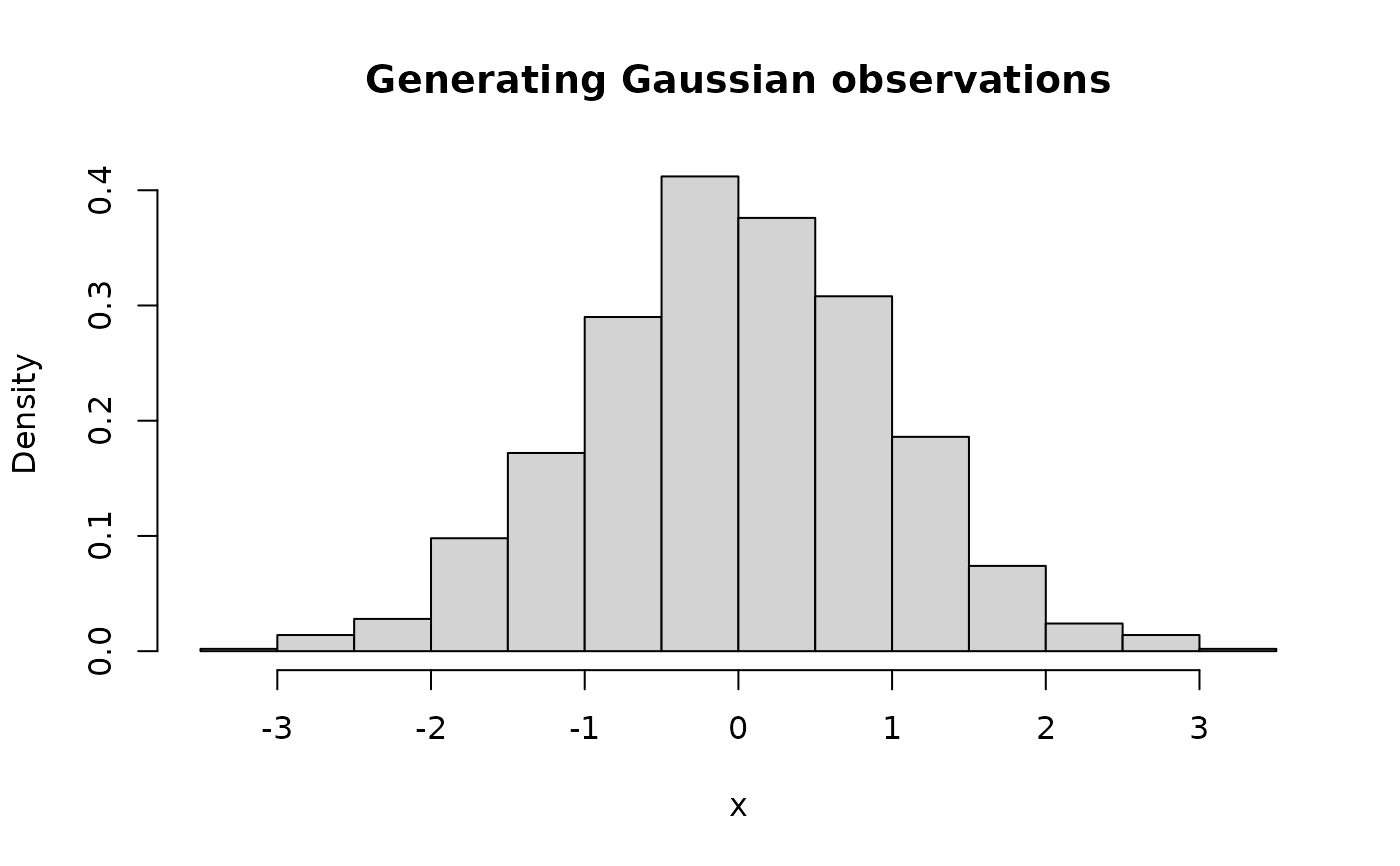
acceptance_rejection(
 n = 1000L,
 f = dnorm,
 continuous = TRUE,
 args_pdf = list(mean = 0, sd = 1),
 xlim = c(-4, 4)
) |>
hist(
  main = "Generating Gaussian observations",
  xlab = "x",
  probability = TRUE
)