Skip to contents

QQ-Plot

Source: vignettes/qqplot.Rmd
qqplot.Rmd

Quantile-Quantile Plot

The package AcceptReject provides the function qqplot.accept_reject() which allows us to construct quantile-quantile plots to assess the goodness of fit of a probability distribution to a data sample. Similar to the function plot.accept_reject(), the function qqplot.accept_reject() is a generic function that accepts an object of class accept_reject as an argument, easily constructing the plot of theoretical quantiles of f against the sample quantiles (observed quantiles).

This function works efficiently, so that in large samples, the points are optimized to generate a more efficient plot, utilizing the scattermore library in R.

General usage format: 

## S3 method for class 'accept_reject'
qqplot(
  x,
  alpha = 0.5,
  color_points = "#F890C2",
  color_line = "#BB9FC9",
  size_points = 1,
  size_line = 1,
  ...
)
  • x: Object of the class accept_reject returned by the function accept_reject().
  • alpha: Transparency of the points and reference line representing where the quantiles should be (theoretical quantiles).
  • color_points: Color of the points (default is "#F890C2").
  • color_line: Color of the reference line (detault is "#BB9FC9").
  • size_points: Size of the points (default is 1).
  • size_line: Thickness of the reference line (default is 1).
  • ...: Additional arguments for the quantile() function. For instance, it’s possible to change the algorithm type for quantile calculation.

Examples

Discrete case 

library(AcceptReject)
#> 
#> Attaching package: 'AcceptReject'
#> The following object is masked from 'package:stats':
#> 
#>     qqplot
library(cowplot)
x <- accept_reject(
  n = 2000L,
  f = dbinom,
  continuous = FALSE,
  args_f = list(size = 5, prob = 0.5),
  xlim = c(0, 5)
)
#> ! Warning: f(5) is 0.03125. If f is defined for x >= 5, trying a upper limit might be better.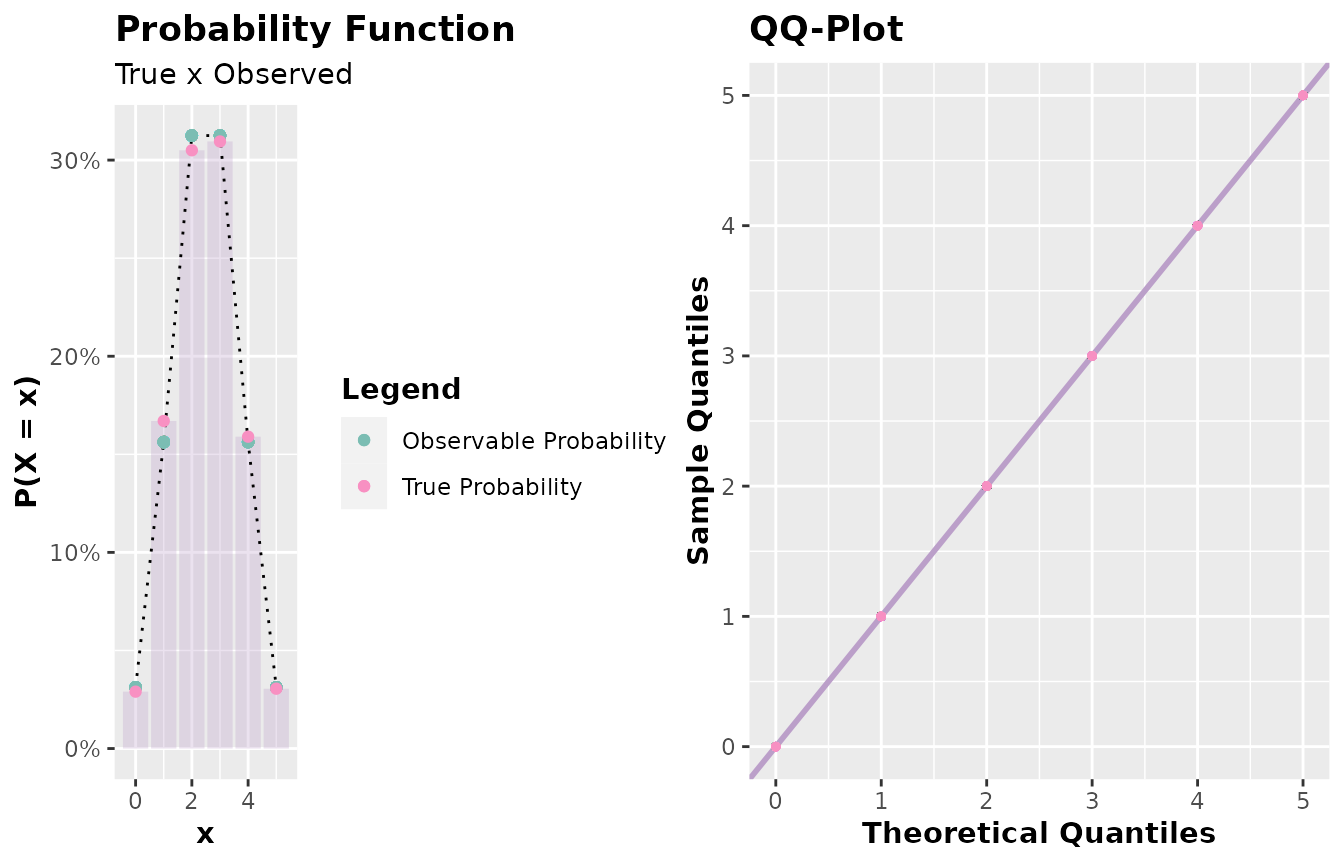
a <- plot(x)
b <- qqplot(x)
plot_grid(a, b, ncol = 2)

Continuous case 

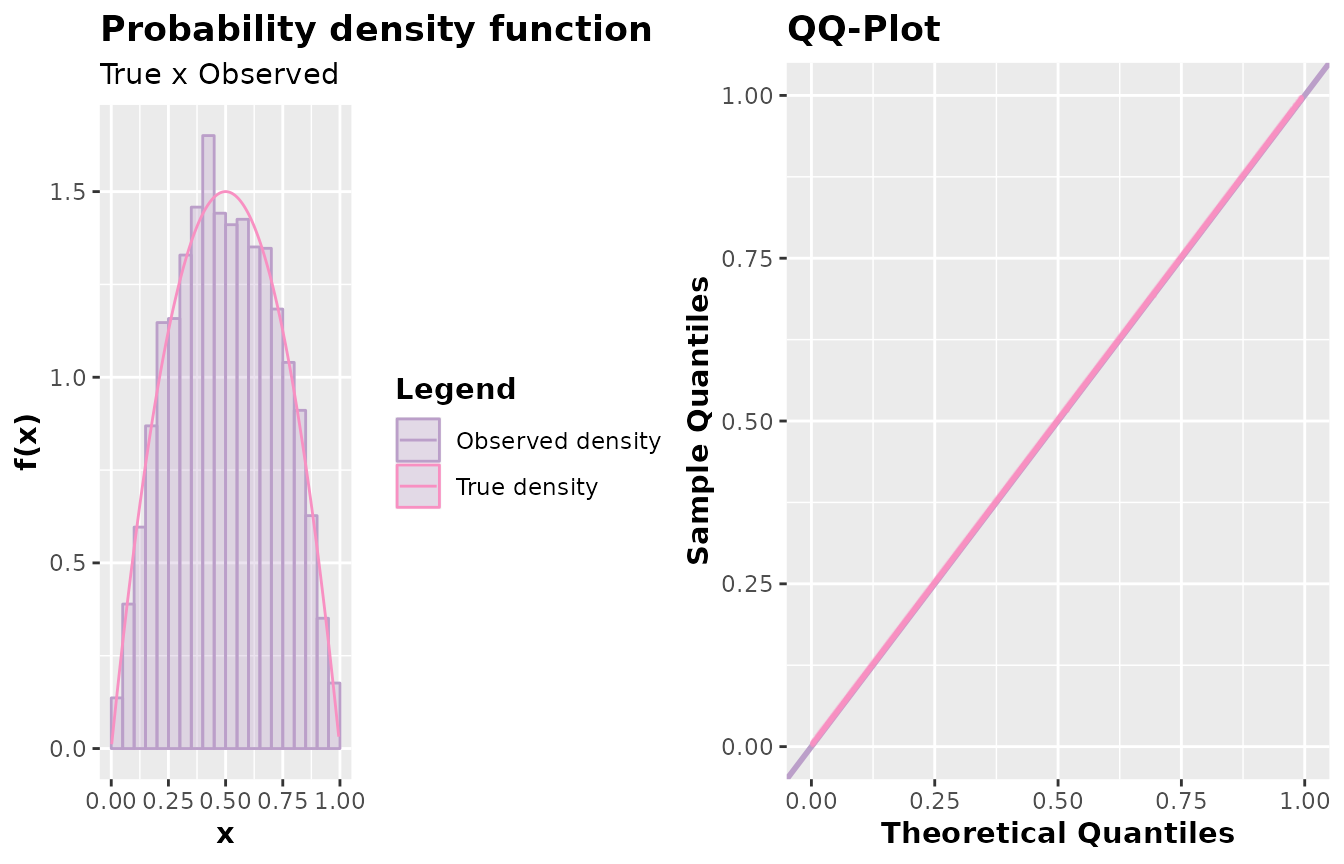
# For n = 1000
y <- accept_reject(
  n = 1000L,
  f = dbeta,
  continuous = TRUE,
  args_f = list(shape1 = 2, shape2 = 2),
  xlim = c(0, 1)
)

# For many points (scattermore is used):
z <- accept_reject(
  n = 11e3,
  f = dbeta,
  continuous = TRUE,
  args_f = list(shape1 = 2, shape2 = 2),
  xlim = c(0, 1)
)

# Gráficos
a <- plot(y)
b <- qqplot(y)
c <- plot(z)
d <- qqplot(z)
plot_grid(a, b, ncol = 2)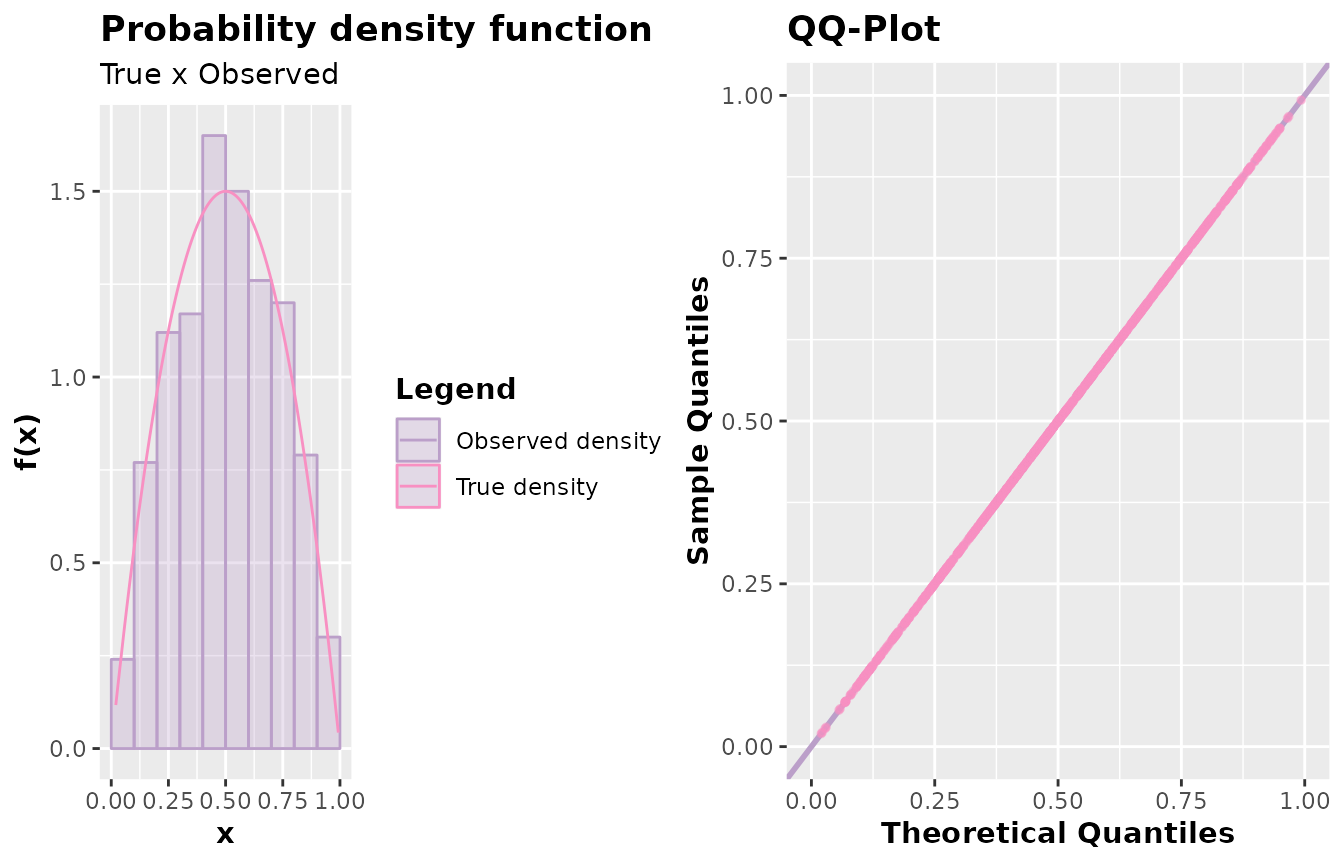

plot_grid(c, d, ncol = 2)